文献阅读笔记-Revisiting a Methodology for Efficient CNN Architectures in Profiling Attacks
文章信息
-
作者:Lennert Wouters, Victor Arribas, Benedikt Gierlichs and Bart Preneel
-
单位:imec-COSIC, KU Leuven Kasteelpark Arenberg 10, B-3001 Leuven-Heverlee, Belgium
-
出处:IACR Transactions on Cryptographic Hardware and Embedded Systems
-
标题:Revisiting a Methodology for Efficient CNN Architectures in Profiling Attacks
文章内容
研究背景
本文主要针对于Zaid在2020年发表论文中的部分论点进行实验取证,构造了不同的网络结构,不同的超参数。
前置知识
数据集
- ASCAD
- DPAv4
- AES_HD
- AES_RD
数据预处理
针对于时间序列分类任务,通常在训练模型之前需要对数据进行预处理,在针对设备进行侧信道攻击时,对于同一种加密操作,同种设备会因电压、温度、测量设备等外界因素而产生细微不同的结果,将采集到的数据通过缩放预处理可以减轻这些噪声带来的影响,在本文中作者最后采用横向预处理技术对数据进行增强。
可视化技术
在模型训练时是无法直接观测到神经网络的具体工作细节的,为了找到对模型结果影响较大的特征点,引入可视化技术来计算输入特征的重要程度。
对于权重可视化方法,主要是针对于展平层FL之后的第一个全连接层:
这里是点处 相对于全连接层的第m个神经元的权重,其中, 这里[flatten -1 ]代表flatten层前的卷积层,也就是卷积层的过滤器数量,就是第一个全连接层的权重,注意: 这里是Zaid论文中展示的计算展平层权重的公式,由于展平层并不涉及训练的权重,本文作者改为对[flatten + 1]也就是全连接层作可视化, 公式如下:
这里是展平层后的全连接层神经元数量
基于扰动的前向传播
基于反向传播
- Layer-wise Relevance Propagation (LRP)
- Gradient * Input
- Integrated Gradients 梯度积分
- DeepLIFT
热图 Heatmaps
感受野
模型结构
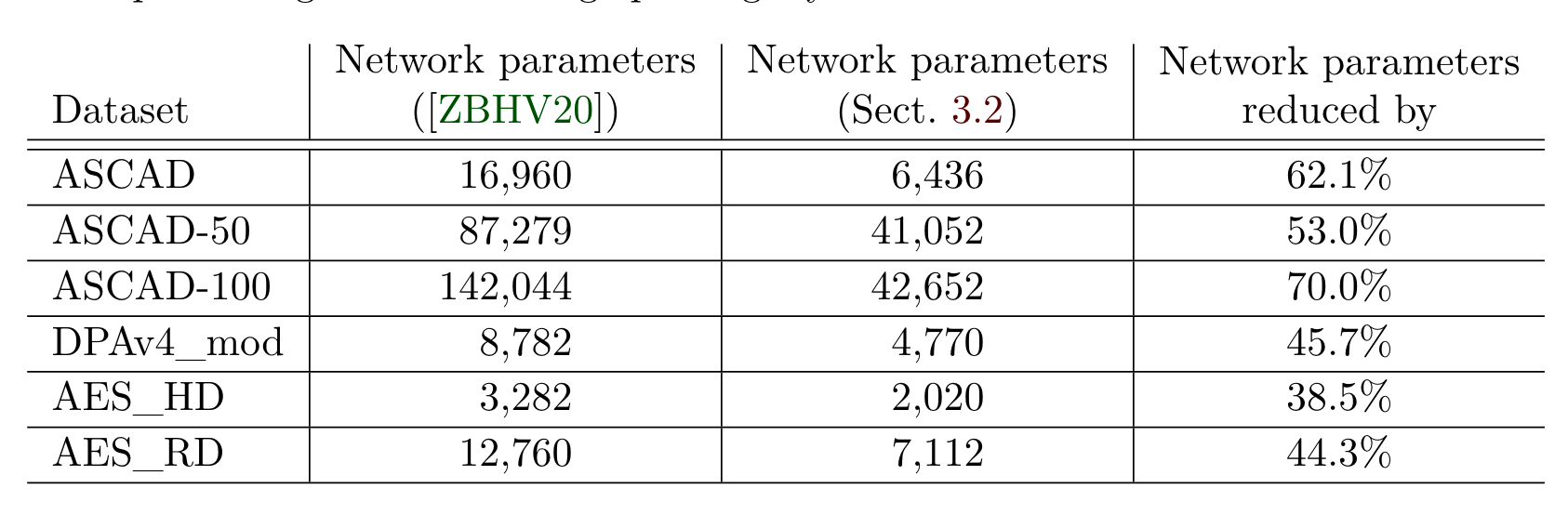
相较于Zaid提出的在输入部分新增卷积核大小为一的卷积层(瓶颈层),作者认为如果采用恰当的数据预处理技术可以省略该层以减少模型的训练参数量,因此作者删除了第一个卷积层和其后边的批量归一化层,但保留池化层,对输入的数据进行降维处理,删除前后训练参数量对比如表1所示。
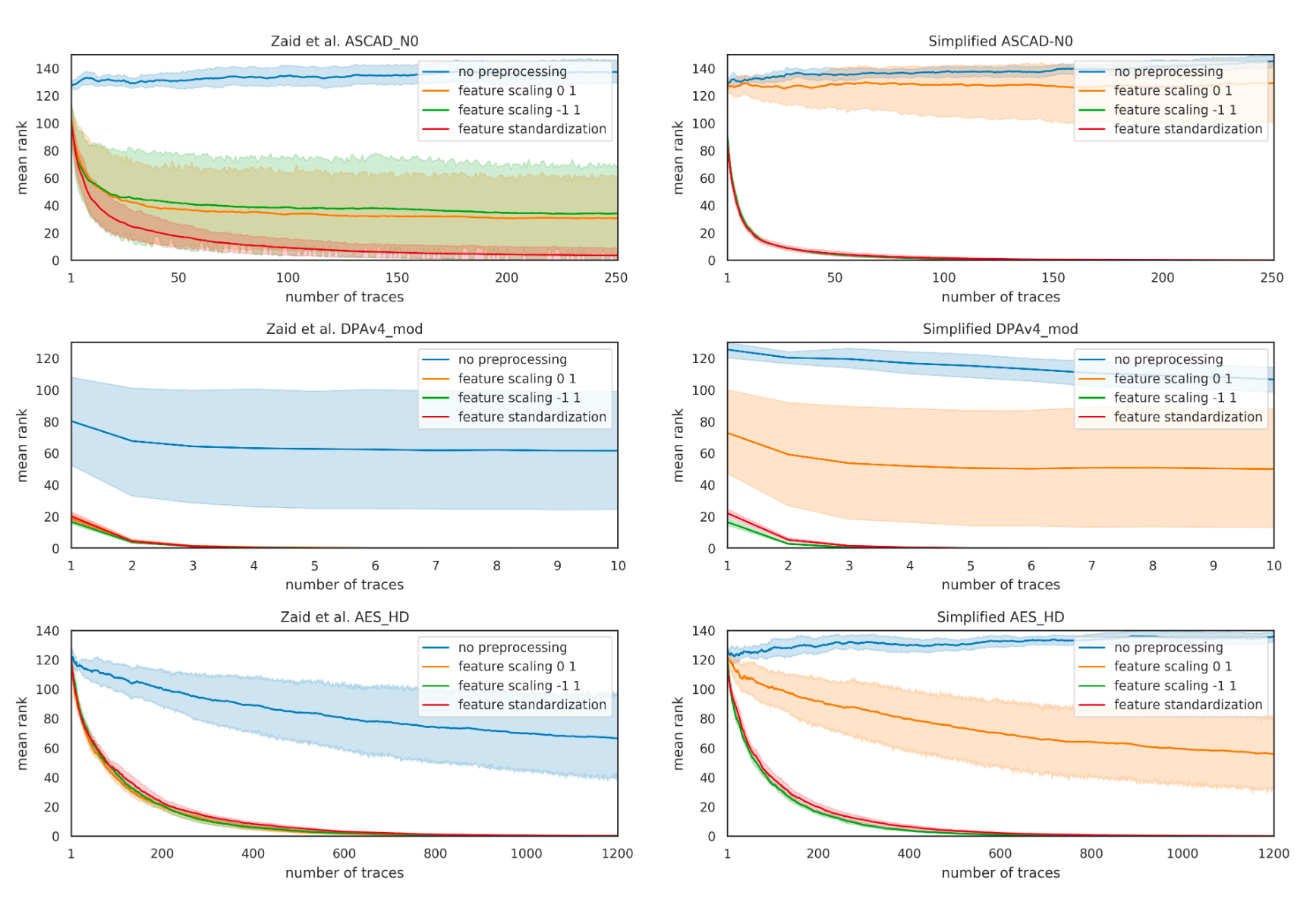
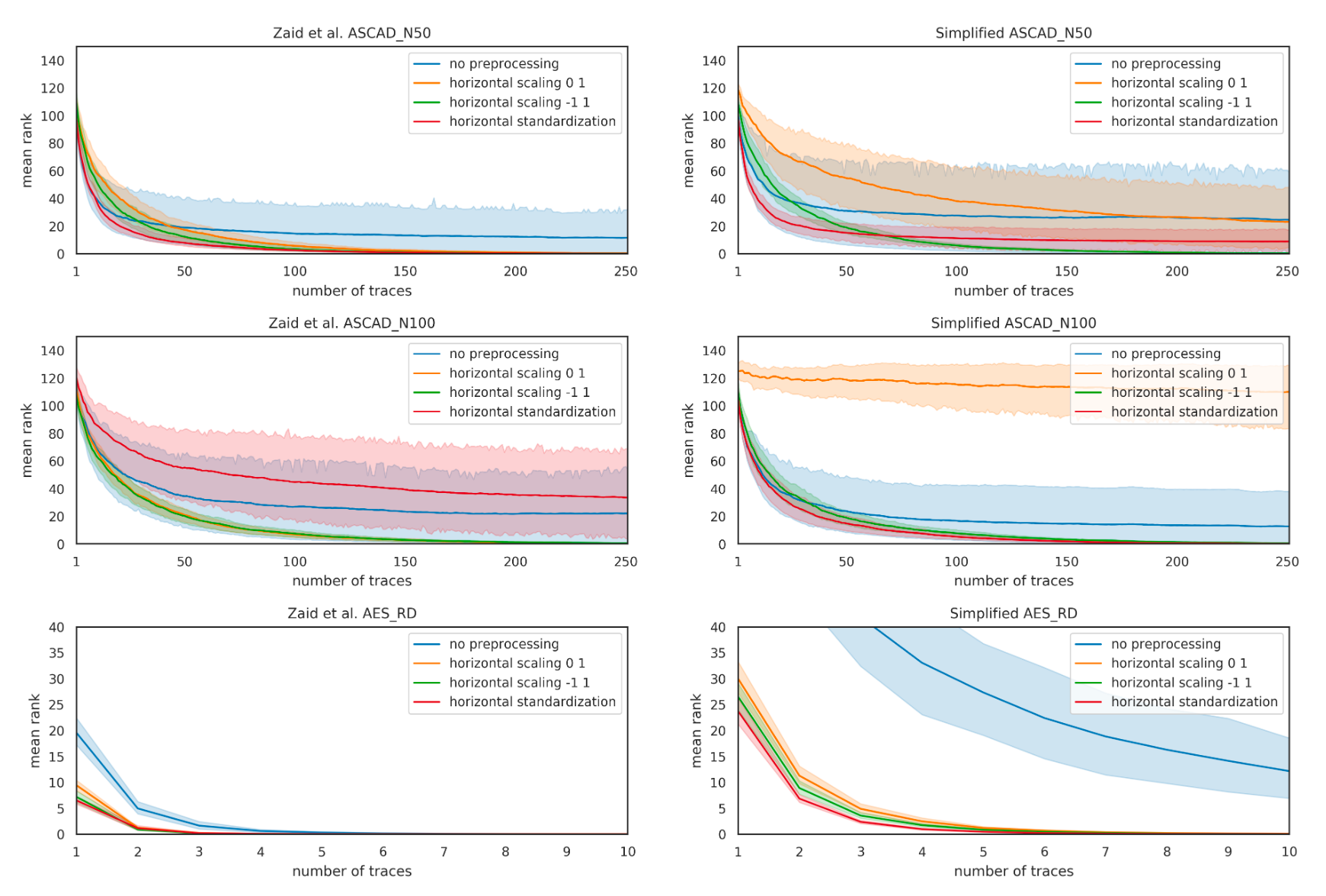
作者结合不同的数据预处理(标准化、缩放)后,用于训练ASCAD能量迹数据集,epoch=50,batchsize=50,lr=0.005,Zaid提出的模型(以下称Zmodel)与简化后的模型(以下称Smodel)猜测熵收敛曲线如图1、图2所示。
作者为了研究批量归一化层对模型的影响,同时删除Zmodel中的批量归一化层,通过新增横向标准化的预处理作对比,在ASCAD N100数据集上 猜测熵收敛曲线如图3所示。
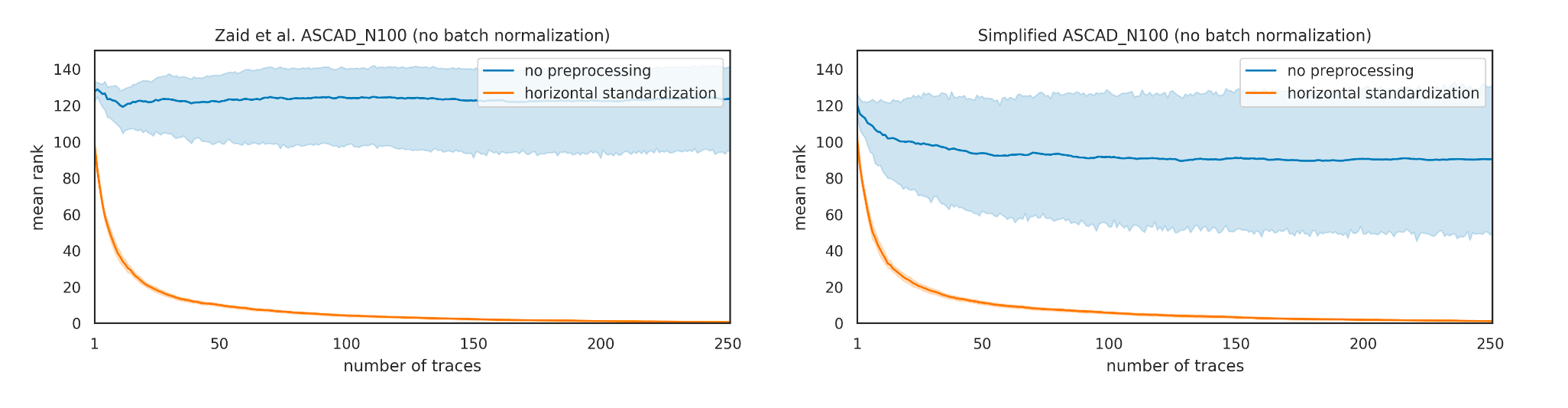
通过以上的实验数据可以得出,在经过横向标准化之后的Smodel与Zmodel在数据集上,在超参数保持一致的前提下,二者收敛曲线类似,模型效果相当
权重可视化方案
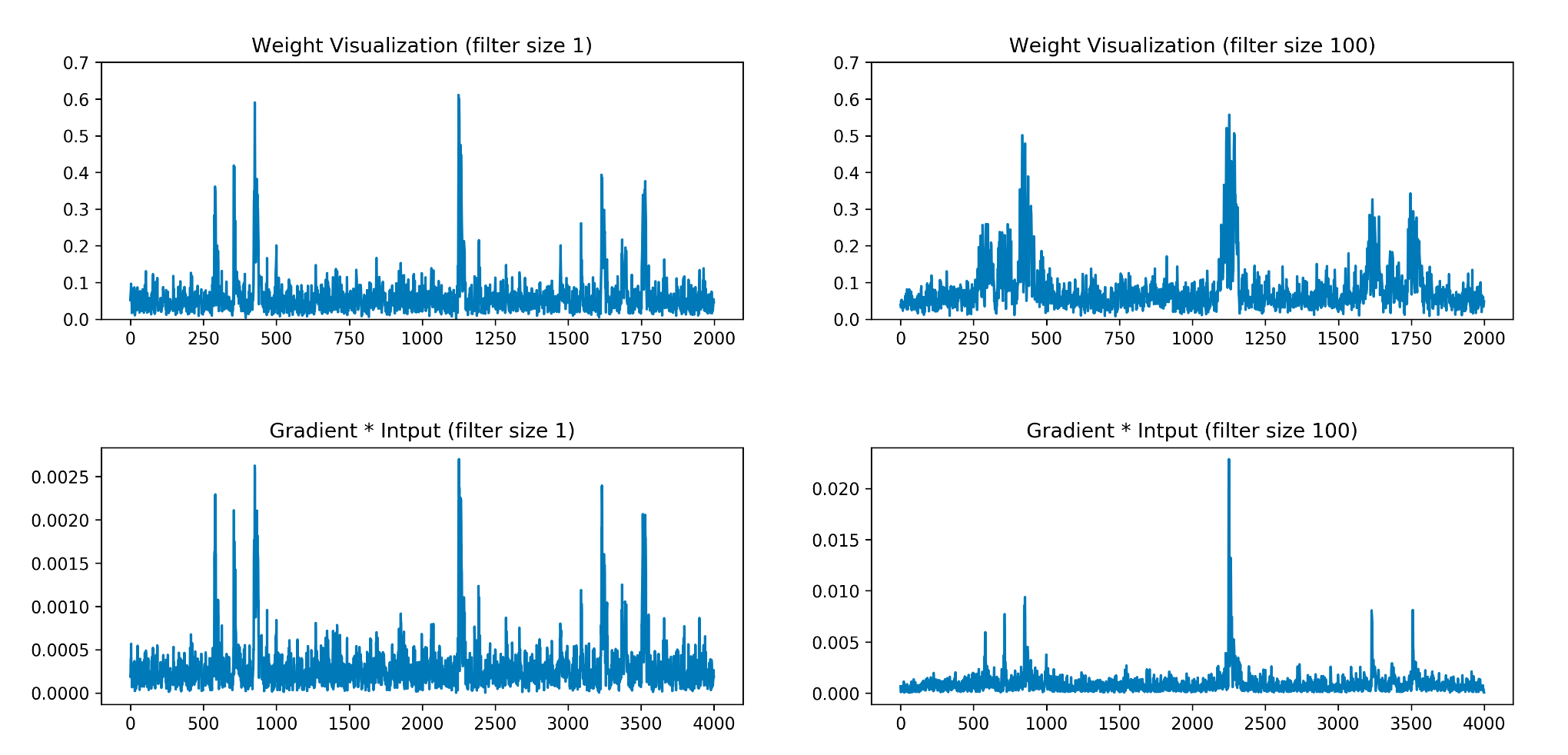
在Zaid等人的研究中,通过第一个全连接层来反映输入数据的权重,本文作者采用梯度*输入来定位兴趣点,在DPAv4数据集上结果如图4所示。可以看到随着过滤器大小的增加,Zaid等人提出的方案会展示出更模糊的兴趣点(权重值大的点变多),而采用梯度*输入方法,则更能精确地反映POI的位置(这里还没有去证实,只是论文里这样说的,但看起来兴趣点似乎确实被更精确地标记了)。如图4、8所示,
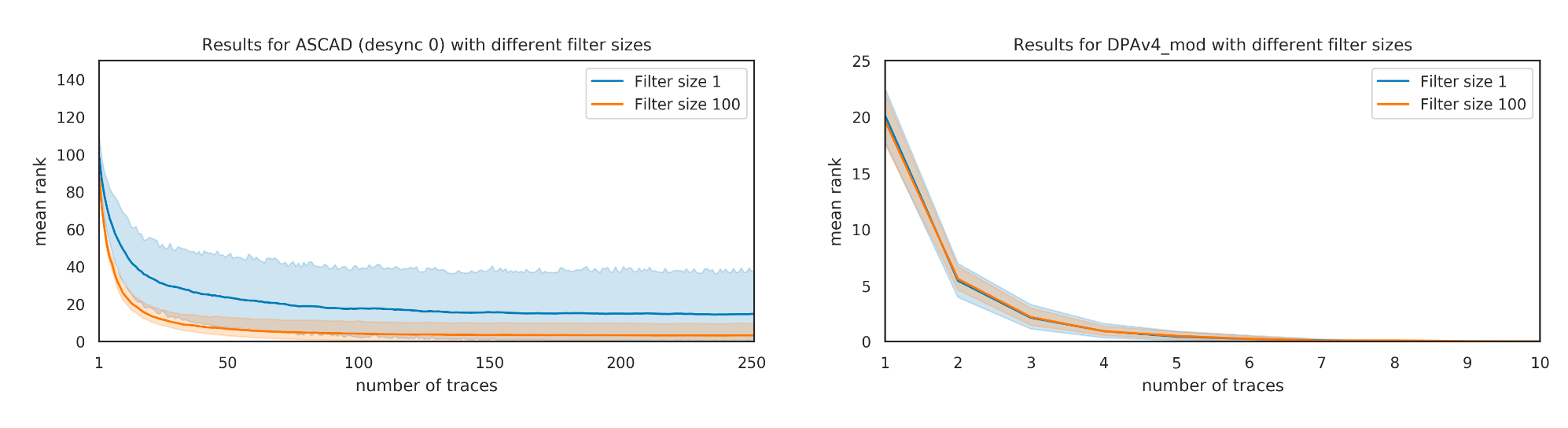
为了证实Zaid的观点(由上可知,Z等人认为过滤器越大会导致模型效果更差)是错误的,作者在DPAv4数据集上针对不同大小为1、100的过滤器做消融实验,收敛曲线如图5所示,可以看到随着过滤器大小的增加,模型收敛效果也越好。
感受野与过滤器大小
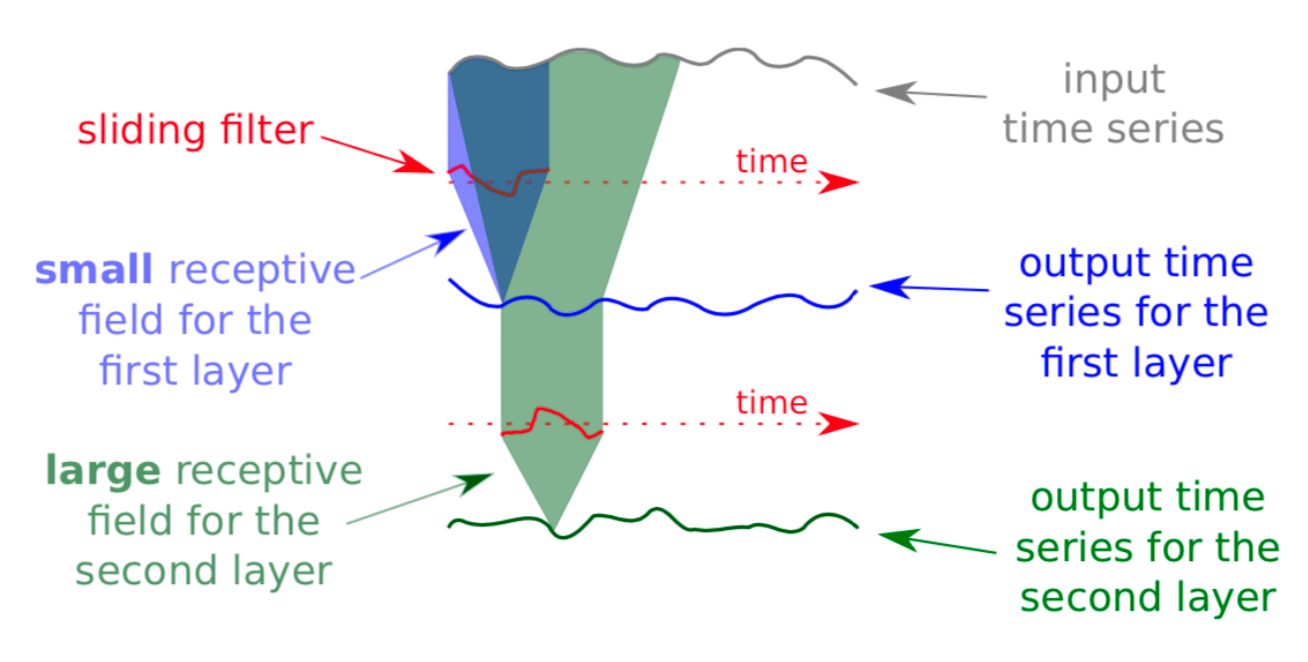
更大的过滤器必然会导致更大的感受野,进而生成稳健性更好的模型,但过大的感受野也会导致巨量的训练参数,因此作者在这里选择不同的过滤器大小来对ASCAD、AES_RD攻击,猜测熵曲线 如图7所示,可以看到增大过滤器的大小会致使收敛效果更好。
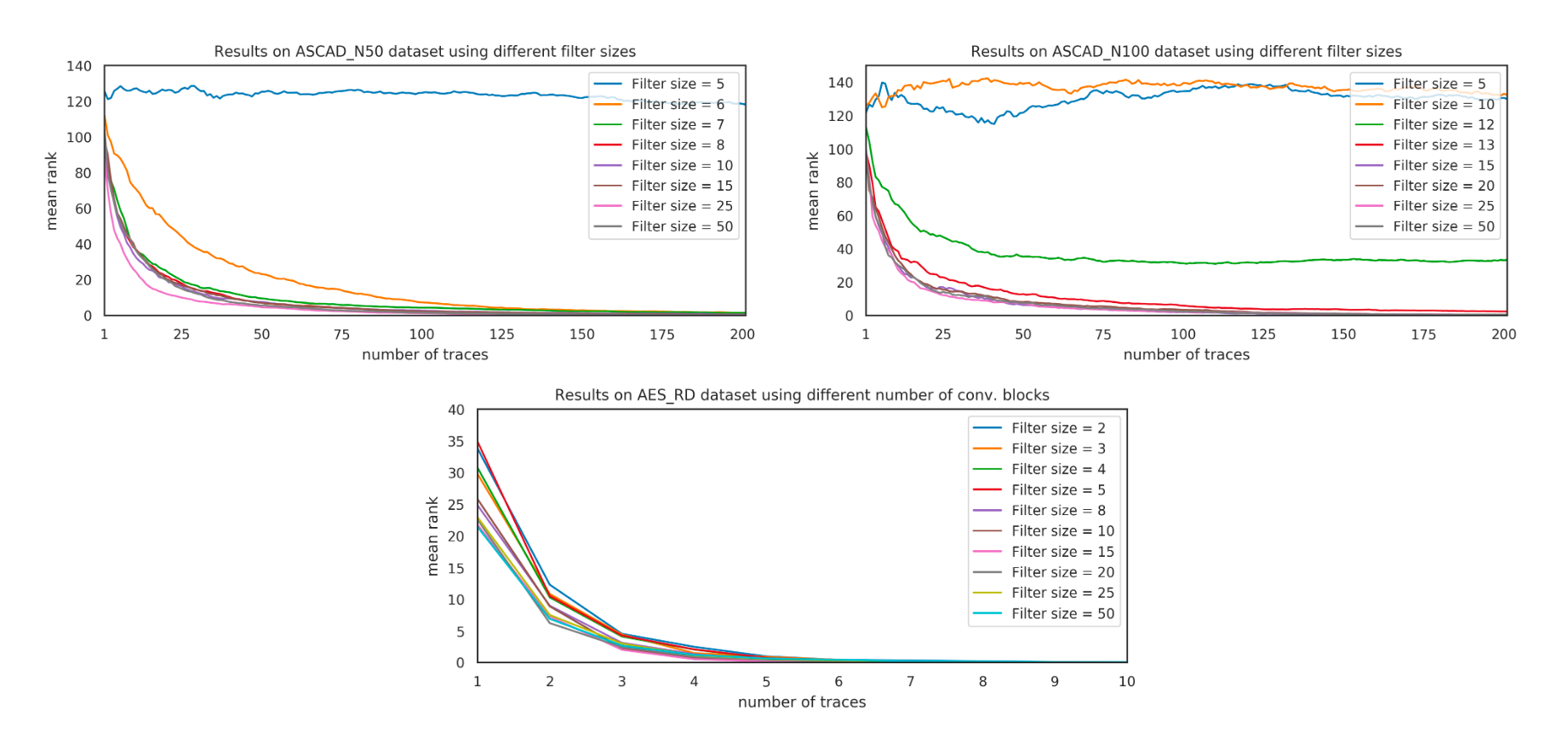
确定卷积块个数
作者为了反驳Zaid的观点(卷积块数量越多模型性能越差),在ASCAD数据集上做消融实验,通过增加卷积块个数对比模型收敛速度,如图9所示,可以看出实验中增加卷积块个数并不会对模型造成负面影响,
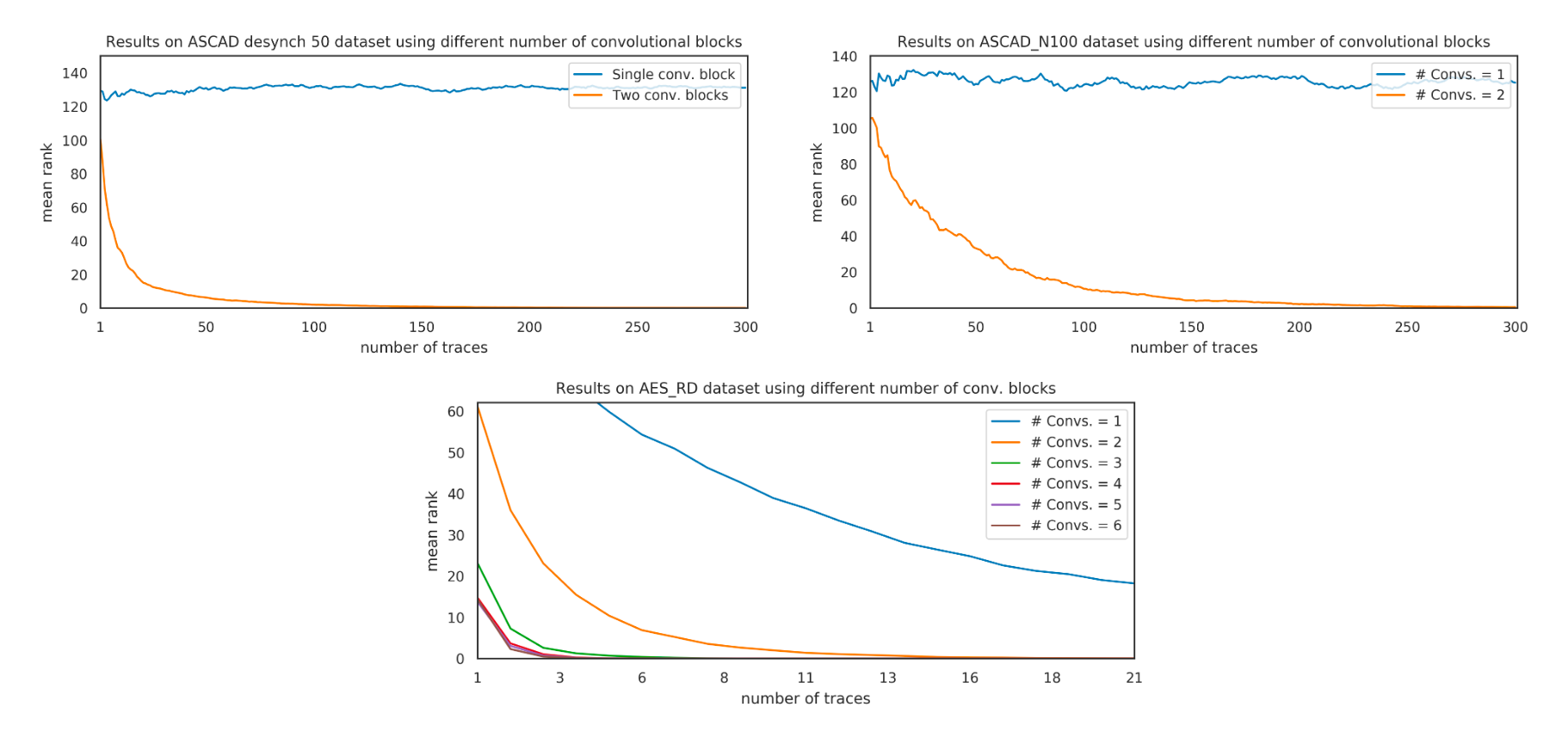
总结
作者在Zaid工作的基础上提出部分相反的观点并证实Zaid等人的错误。
- 在Zaid等人提出的模型基础上进行简化,去掉第一个卷积层、归一化层,保留池化层。
- 在训练开始前对数据进行横向标准化处理。
- 找到权重可视化技术 梯度*输入来证明Zaid等人的工作是错误的,但也指出利用这种技术并不能直接证明模型的好坏。
- 反驳Zaid等人的纠缠观点,这里纠缠是指模型越深效果越差。
- 找到简化模型的合适超参数。
