文章信息

  • 作者：Guilherme Perin1,2, Lichao Wu2 and Stjepan Picek1
  • 单位：
    • 1 Radboud University, Nijmegen, The Netherlands picek.stjepan@gmail.com
    • 2 Delft University of Technology, Delft, The Netherlands {G.Perin,L.Wu-4}@tudelft.nl
  • 出处：IACR Transactions on Cryptographic Hardware and Embedded Systems
  • 标题：Exploring Feature Selection Scenarios for Deep Learning-based Side-channel Analysis

文章内容

研究背景

近年来，深度学习技术在侧信道攻击（Side Channel Attack，SCA）领域取得了显著的进展，侧信道分析是一种通过对加密设备的物理特性（如功耗、电磁辐射等）来推断密钥信息的方法。一般而言，侧信道攻击需要人为挑选特征区间，即从大量的时间样本点中挑选与密钥相关的部分。这就要求攻击者在建模阶段之前的随机掩码已知，以此来计算信噪比等相关指标。

例如在ASCAD数据集上，攻击已经修剪好的700个样本点时，尽管研究者们在建模、攻击阶段避免使用到随机掩码的先验知识，但不可避免的是，在使用700个点时，实际上已经默认掩码已知。因为在裁剪这些样本点区间时，原作者利用到了掩码的知识来完成信噪比的计算，以此来挑选出了与密钥相关的这部分。

Lu等人[1]首先提出了一种端到端的侧信道攻击方法，堆叠多层不同的神经网络对原始能量迹完成攻击，无需对数据进行特征选择，从而避免使用到有关随机掩码的先验知识。但模型存在复杂度过高的问题，在本文中作者提出利用结构较为简单的模型在无特征选择的条件下来完成攻击。

感知信息（PI）[2]

与猜测熵和成功率应用场景相同，PI也被用作评估模型的好坏，以此来衡量模型可以从样本点中获取多少有用的信息，并通过样本数量来计算攻击的复杂度。PI的计算公式如下：

PI^(X,Y)=H(Y)+∑y∈Yp(y)1Ny∑iNylog⁡2p^(y∣xiy)\widehat{PI}(X,Y)=H(Y)+\sum_{y\in{Y}}p(y)\frac{1}{N_y}\sum_{i}^{N_y}\log_2\hat{p}(y\mid{x_{i}^{y}})

其中，p^(y∣xiy)\hat{p}(y\mid{x_{i}^{y}})是模型对样本xiyx_{i}^{y}预测的属于标签yy的概率。Measure等人[3]证明了交叉熵损失函数的最小化类似于最大化的感知信息。PI给出了攻击所需能量迹数量的边界N^β,PI\hat{N}_{\beta,PI}。

N^β,PI≥f(β)PI^(X,Y)\hat{N}_{\beta,PI} \ge \frac{f(\beta)}{\widehat{PI}(X,Y)}

f(β)f(\beta)[4]是一个与期望成功率β\beta相关的较小的常数，这里只在β\beta等于0.8时计算ff，也就是成功率等于百分之八十。f(β)f(\beta)的计算公式如下：

f(β)=n−(1−β)log⁡2(2n−1)+βlog⁡2(β)+(1−β)log⁡2(1−β)=n−0.2log⁡2(2n−1)+0.8log⁡2(0.8)+0.2log⁡2(0.2)\begin{aligned} f(\beta) &=n-(1-\beta)\log_2(2^n-1)+\beta\log_2(\beta)+(1-\beta)\log_2(1-\beta)\\ &=n-0.2\log_2(2^n-1)+0.8\log_2(0.8)+0.2\log_2(0.2)\\ \end{aligned}

相关工作

在侧信道攻击中，原始能量迹往往会包含大量特征的原始能量迹。为了降低攻击难度，数据集提供者往往会给出一个修剪后的数据集，选择包含对应密钥字节操作的兴趣点且较小的区间范围，而这个选择的过程是基于掩码已知的知识来完成的。

在文献[5]中，作者通过卷积神经网络来完成在大规模原始能量迹上（包含16w个时间样本点）的攻击，Lu等人[6]完成ASCAD、DPAv4.2数据集中基于原始能量迹的攻击。在Lu等人的工作中，作者通过堆叠长短期记忆网络、注意力机制、卷积块来完成模型的构建，模型较为复杂。对此，本文提出了基于简单结构的神经网络模型来恢复密钥字节的方法。

研究方法

作者介绍了三种攻击场景：

  1. 最坏假设（OPOI）：掩码已知
  2. 弱假设（RPOI）：掩码未知
  3. 真实场景（NOPOI）：原始能量迹且掩码未知
数据集 RPOI OPOI NOPOI 原始能量迹样本点总数量
ASCADf 包含信噪比峰值的1 000个样本点区间 [45 400:46 100] [0:100 000] 100 000
ASCADr 包含信噪比峰值的1 000个样本点区间 [80 945:82 345] [0:250 000] 250 000
DPAv4.2 包含信噪比峰值的1 000个样本点区间 [170 000:174 000, 206 000:210 000] [250 000: 400000] 1 700 000
CHESCTF - [0:10 000, 120 000:150 000] [0:150 000] 650 000

RPOI

在RPOI场景下，作者的目标是为了验证神经网络模型具有在该数据集上完成攻击的能力，根据掩码选择包含有用信息的信噪比峰值的样本点区间。此外，选择高斯模板攻击、MLP、CNN作对比，并且对比有无LDA降维方案得攻击效果，具体如图1所示。

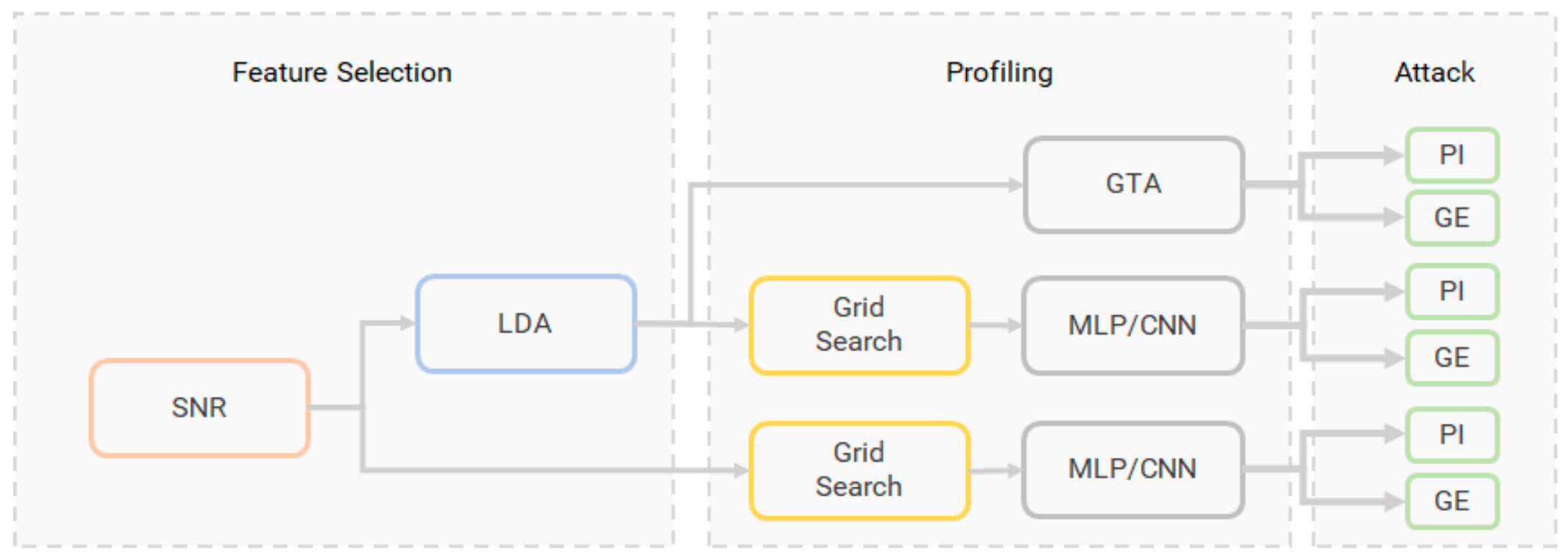
图1 RPOI场景流程图

OPOI

假设掩码已知，在OPOI的场景下主要考虑包含带掩码的泄露Sbox(pi⊕ki)⊕rS_{box}(p_i\oplus k_i)\oplus r与rr的最高信噪比的样本点区间，但是在攻击时并不加入已知掩码这一背景知识。

NOPOI

在文献[6:1]中已经考虑过在原始能量迹上无已知掩码的场景，尽管已经有较好的攻击结果，但模型复杂度过高，训练内存要求过大。在原始能量迹上直接发起攻击也许并不适合真实的场景，本文考虑在训练前执行下采样预处理，窗口大小分别为10、20、40以及80，且保证有50%的重叠区间。此外，对DPAv42以及CHESCTF_2018，作者仅考虑在第一轮AES加密对应的时间样本点区间。

模型选择方案

MLP

超参数 随机搜索 网格搜索
优化器 Adam,RMSprop Adam,RMSprop
Dense层 1,2,3,4,5,6,7,8 1,2,3
神经元个数 10,20,50,100,200,300,400,500 20,50,100,200
激活函数 SeLU,ReLU SeLU,ReLU
学习率 1e-3,1e-4,5e-3,5e-4 1e-3,1e-4
Batch Size 100 To 1 000 (步长：10) 200,400
权重初始化方案 ramdom,glorot, he_uniform Glorot
正则 Dropout,None,l1,l2 None
搜索空间 5 971 968 192

CNN

超参数 随机搜索 网格搜索
优化器 Adam,RMSprop Adam,RMSprop
卷积层 1,2,3,4 1
滤波器数量 4∗2i−1,8∗2i−1,12∗2i−1,16∗2i−1,i=层数索引4*2^{i-1}, 8*2^{i-1}, 12*2^{i-1}, 16*2^{i-1},i=层数索引 5,10
卷积核大小 26 To 52 （步长：2） 2,4
池化类型 Maxpooling，AvgPooling AvgPooling
池化层大小 2,4,6,8,10 2
池化层步长 与层大小相同 2
Dense层数 1,2,3,4 1,2
神经元个数 10,20,50,100,200,300,400,500 50,100
激活函数 SeLU,ReLU SeLU,ReLU
学习率 1e-3,1e-4,5e-3,5e-4 1e-3,1e-4
Batch Size 100 To 1 000 (步长：10) 200,400
权重初始化方案 ramdom,glorot, he_uniform Glorot
正则 Dropout,None,l1,l2 None
搜索空间 >1B 128

实验结果及分析

图太多了，这里只给出最关键的NOPOI在三个不同数据集上的攻击结果（将猜测熵收敛到1所需要的能量迹条数）。

表1 ASCADf 表2 ASCADr 表3 DPAv4.2 表4 CHESCTF_2018

总览：

所有结果

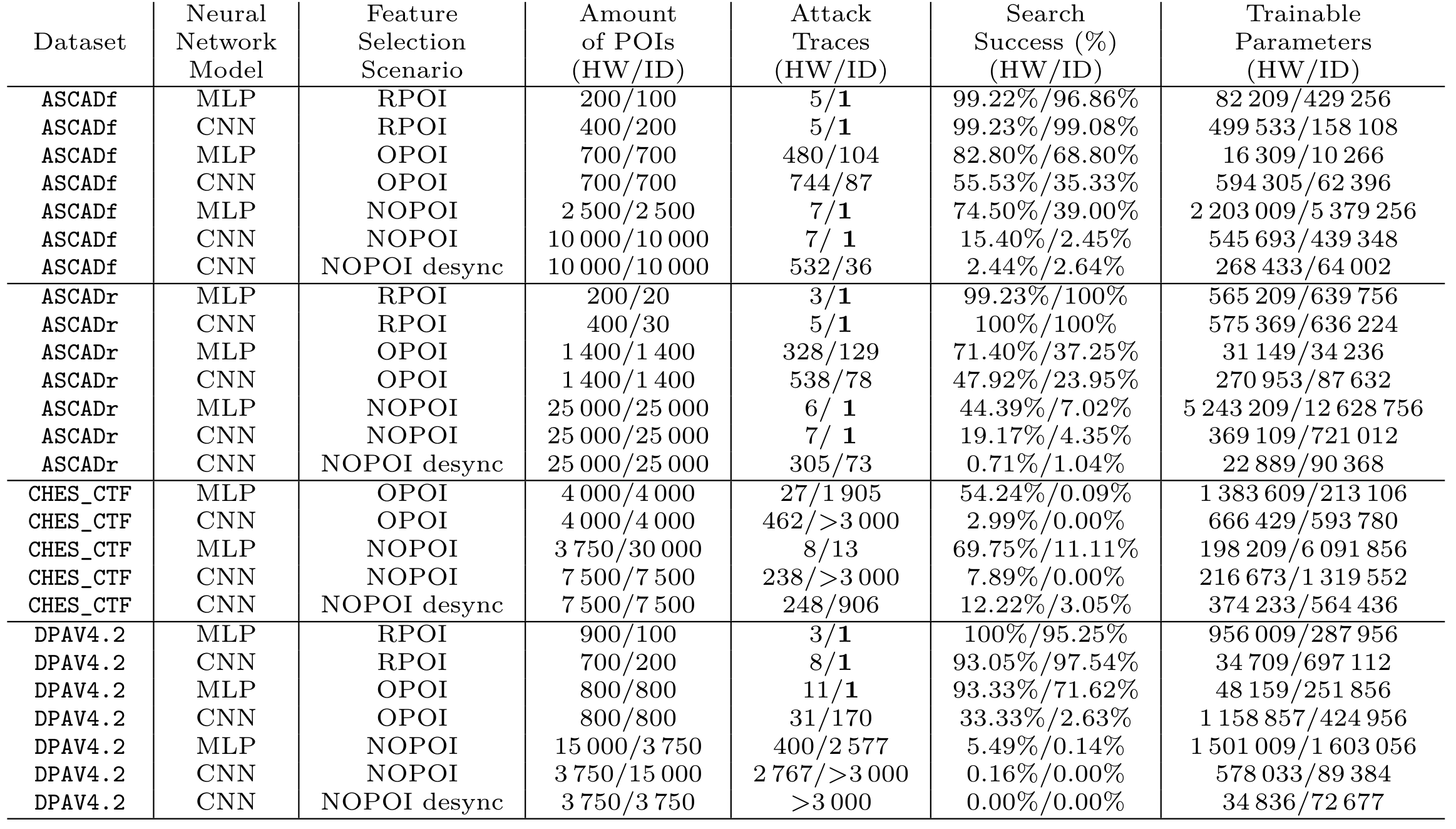
总结

本文主要提供了一个在原始能量迹上完成攻击的方案，改进了Lu等人的模型，在模型复杂度较低的前提下保证了攻击的效果。此外，作者做了大量的对比实验，论文代码：https://github.com/AISyLab/feature_selection_dlsca

参考文献

  1. Xiangjun Lu, Chi Zhang, Pei Cao, Dawu Gu, and Haining Lu. Pay attention to raw traces: A deep learning architecture for end-to-end profiling attacks. IACR Trans. Cryptogr. Hardw. Embed. Syst., 2021(3):235–274, 2021. ↩︎

  2. Olivier Bronchain, Julien M. Hendrickx, Clément Massart, Alex Olshevsky, and François-Xavier Standaert. Leakage certification revisited: Bounding model errors in side-channel security evaluations. In Alexandra Boldyreva and Daniele Micciancio, editors, Advances in Cryptology - CRYPTO 2019 39th Annual International Cryptology Conference, Santa Barbara, CA, USA, August 18-22, 2019, Proceedings, Part I, volume 11692 of Lecture Notes in Computer Science, pages 713–737. Springer, 2019. ↩︎

  3. Loïc Masure, Cécile Dumas, and Emmanuel Prouff. A comprehensive study of deep learning for side-channel analysis. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2020(1):348–375, Nov. 2019. ↩︎

  4. Eloi de Chérisey, Sylvain Guilley, Olivier Rioul, and Pablo Piantanida. Best information is most successful mutual information and success rate in sidechannel analysis. IACR Trans. Cryptogr. Hardw. Embed. Syst., 2019(2):49–79, 2019. ↩︎

  5. Loïc Masure, Nicolas Belleville, Eleonora Cagli, Marie-Angela Cornelie, Damien Couroussé, Cécile Dumas, and Laurent Maingault. Deep learning side-channel analysis on large-scale traces - A case study on a polymorphic AES. In Liqun Chen, Ninghui Li, Kaitai Liang, and Steve A. Schneider, editors, Computer Security - ESORICS 2020 - 25th European Symposium on Research in Computer Security, ESORICS 2020, Guildford, UK, September 14-18, 2020, Proceedings, Part I, volume 12308 of Lecture Notes in Computer Science, pages 440–460. Springer, 2020. ↩︎

  6. Xiangjun Lu, Chi Zhang, Pei Cao, Dawu Gu, and Haining Lu. Pay attention to raw traces: A deep learning architecture for end-to-end profiling attacks. IACR Trans. Cryptogr. Hardw. Embed. Syst., 2021(3):235–274, 2021. ↩︎ ↩︎