文章信息

  • 作者：Lichao Wu, Guilherme Perin and Stjepan Picek
  • 单位：Radboud University, The Netherlands; Delft University of Technology, The Netherlands
  • 出处：IACR Transactions on Cryptographic Hardware and Embedded Systems
  • 标题：The Best of Two Worlds: Deep Learning-assisted Template Attack

文章代码链接

最近开题，开完无缝衔接流感，服啦！

文章内容

作者提出了基于相似性学习的特征提取方法， 使用三元组模型来实现；提出一种新的mertic来提高提取的特征质量

相似性学习（Similarity Learning）

相似性学习属于监督学习，其目的是为了通过训练来计算两实体之间的相似性，可以通过选择三元组模型来完成该任务。

三元组

三元组由三种样本进行输入：正样本、负样本和锚点样本。其中正样本Positive与锚点样本Anchor具有相同的标签，

  1. 损失函数

loss=max(d(a,p)−d(a,n)+margin,0)loss = max(d(a, p) - d(a, n) + margin, 0)

d表示特征向量之间的欧氏距离，aa表示锚点，pp表示正样本，ｎｎ表示负样本，marginmargin 是阈值用来控制正负样本之间的距离。

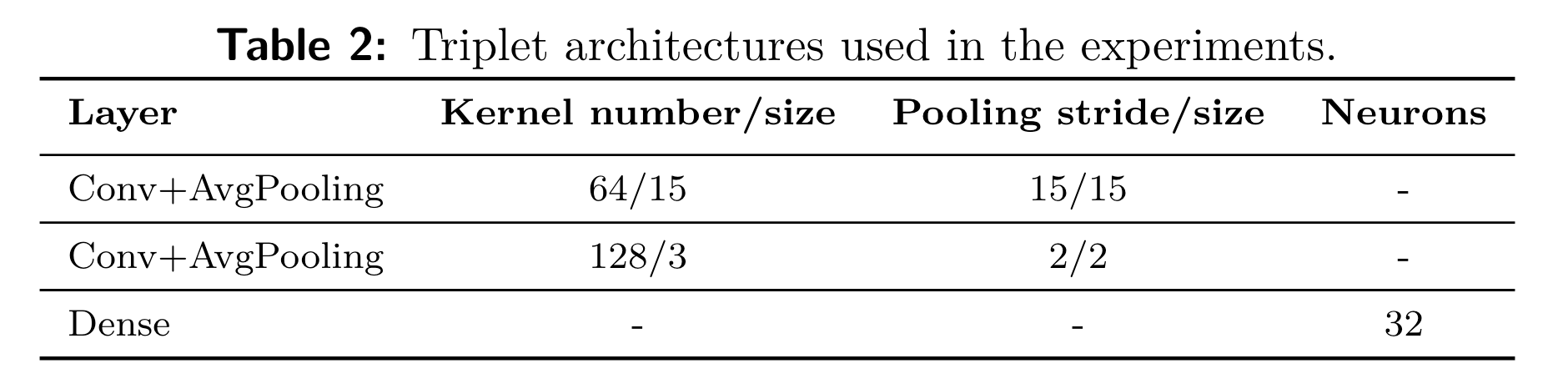
三元组分为三类，网络结构如图1所示，本文作者将marginmargin设置为0.4：

类别 关系
正样本三元组 d(ra,rn)>d(ra,rp)+md(r_a, r_n) > d(r_a,r_p) + m 正负样本距离足够大 (>m)，此时loss = 0，网络不再更新
负样本三元组 d(ra,rn)<d(ra,rp)d(r_a,r_n) < d(r_a,r_p) 负样本与锚点的距离比正样本更近，此时loss>0, 网络继续更新
中等样本三元组 d(ra,rp)<d(ra,rn)<d(ra,rp)+md(r_a,r_p)<d(r_a,r_n)<d(r_a,r_p) + m负样本到锚点距离虽然大于正样本到锚点的，但是没要大于阈值m，此时loss仍然大于0，网络继续更新
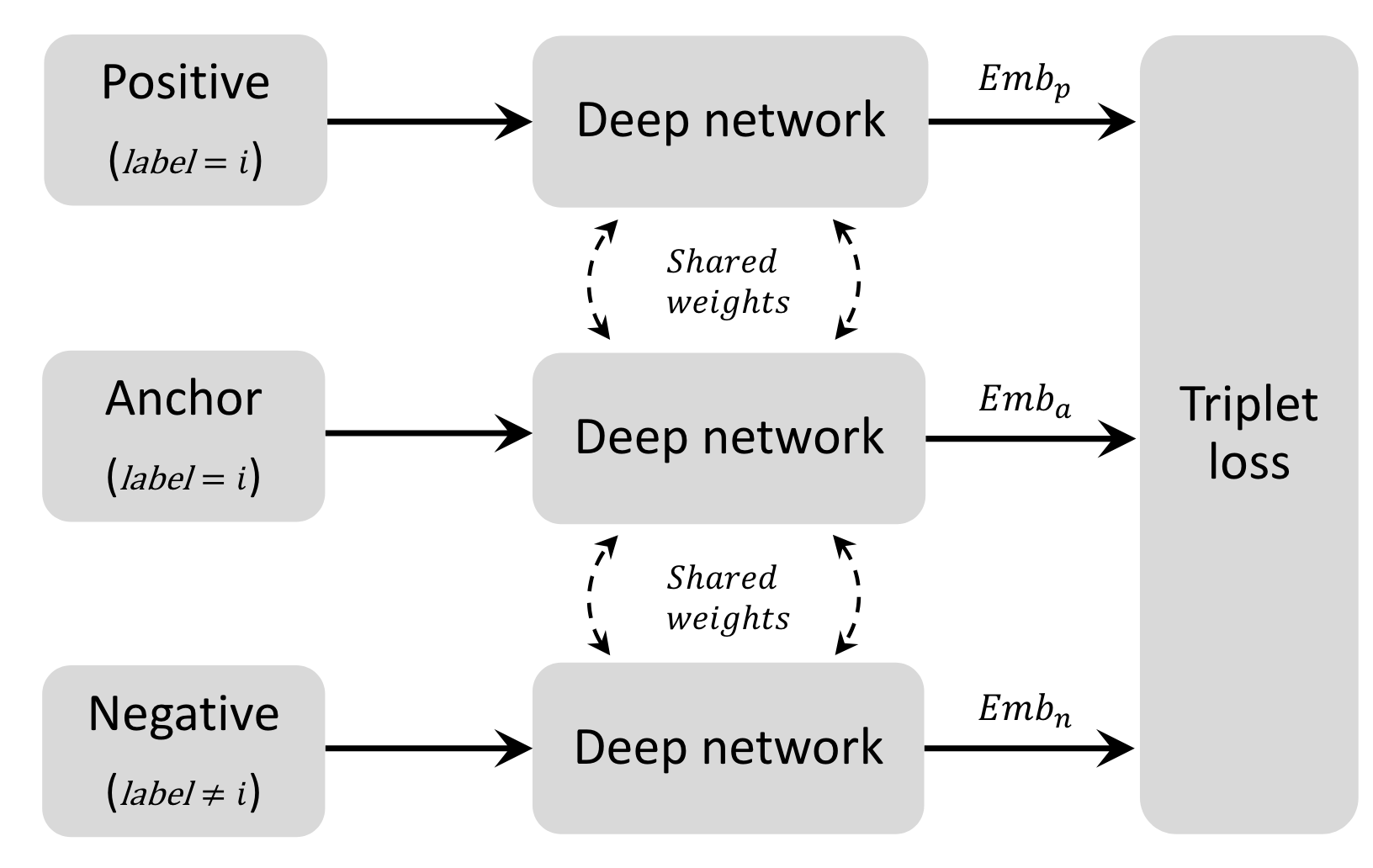
图1 三元组网络结构

基于混合距离的三元组损失

原始三元组方案忽略了负样本中的标签多样性，即对具有C个类别的数据集，负样本包含C-1个类别，作者认为如果在中等样本三元组中采用负样本的标签信息来寻找最接近锚点的负样本点，包含这种距离进的负样本点会促使模型学习效率会更好，分类性能提升更大。

虽然在CV领域不能通过标签来判断负样本点与锚点的相似性，但是侧信道攻击中是可以的（相似的标签可能是相似的泄漏点导致的），由此作者给出了基于混合距离的三元组损失函数如图2，其中 dd 表示欧氏距离的平方，la,lbl_a,l_b表示对应标签，d′d^{\prime}表示标签归一化后的欧氏距离，

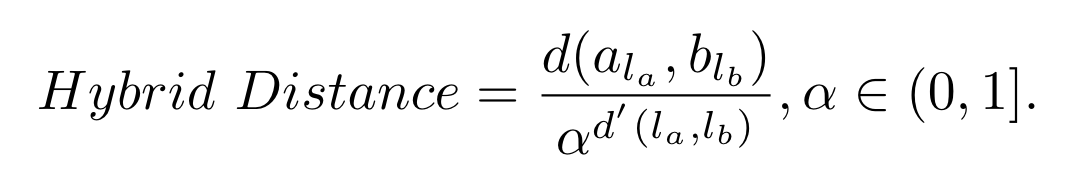
图2 混合距离

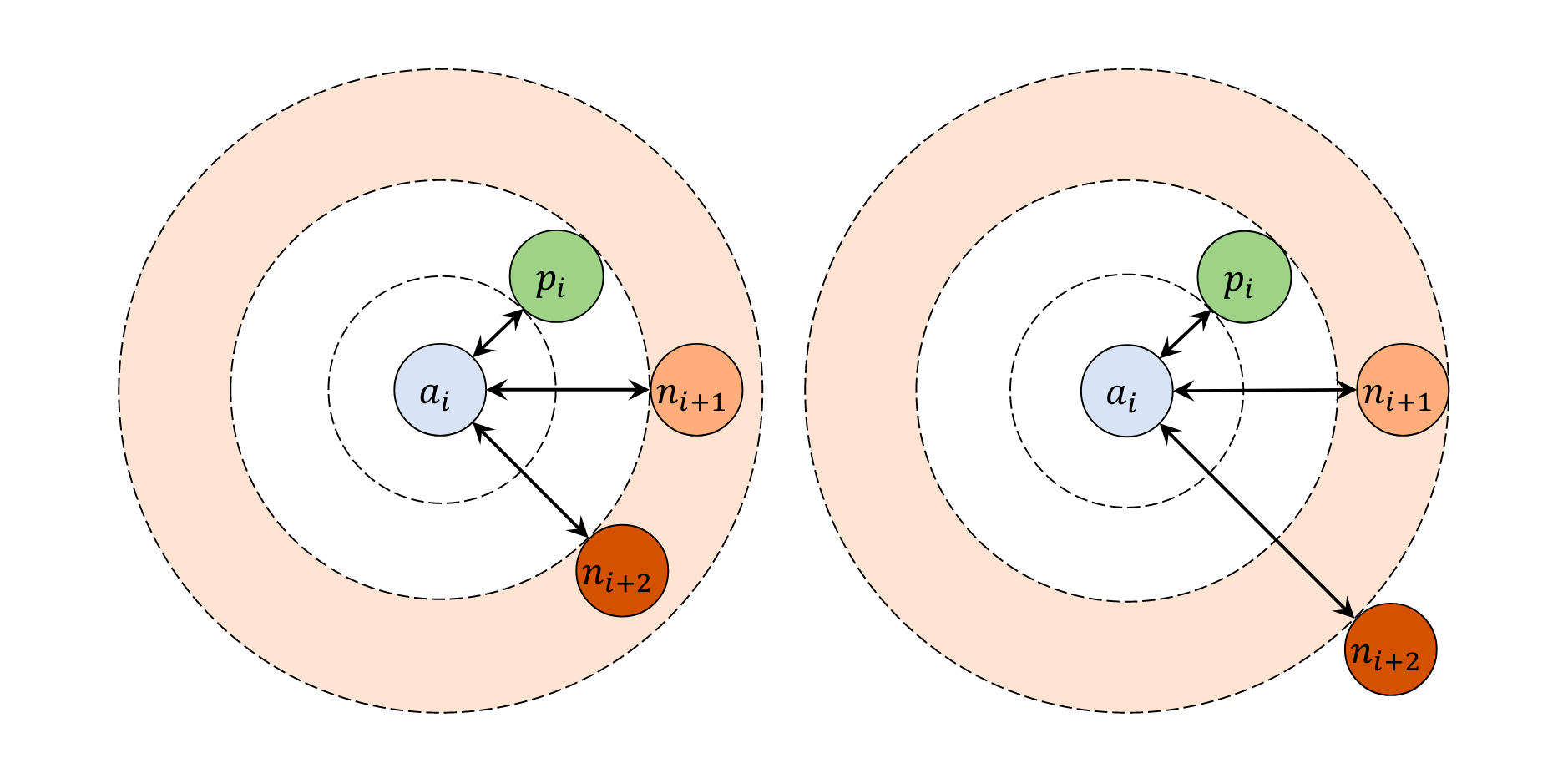
图三展示了在基于中等样本三元组情况下，欧氏距离与混合距离三元组损失的区别，即相较于传统欧氏距离，混合距离（右图）将不考虑ni+2n_{i+2}，只在ni+1n_{i+1}上学习。

图3 欧氏距离与混合距离区别

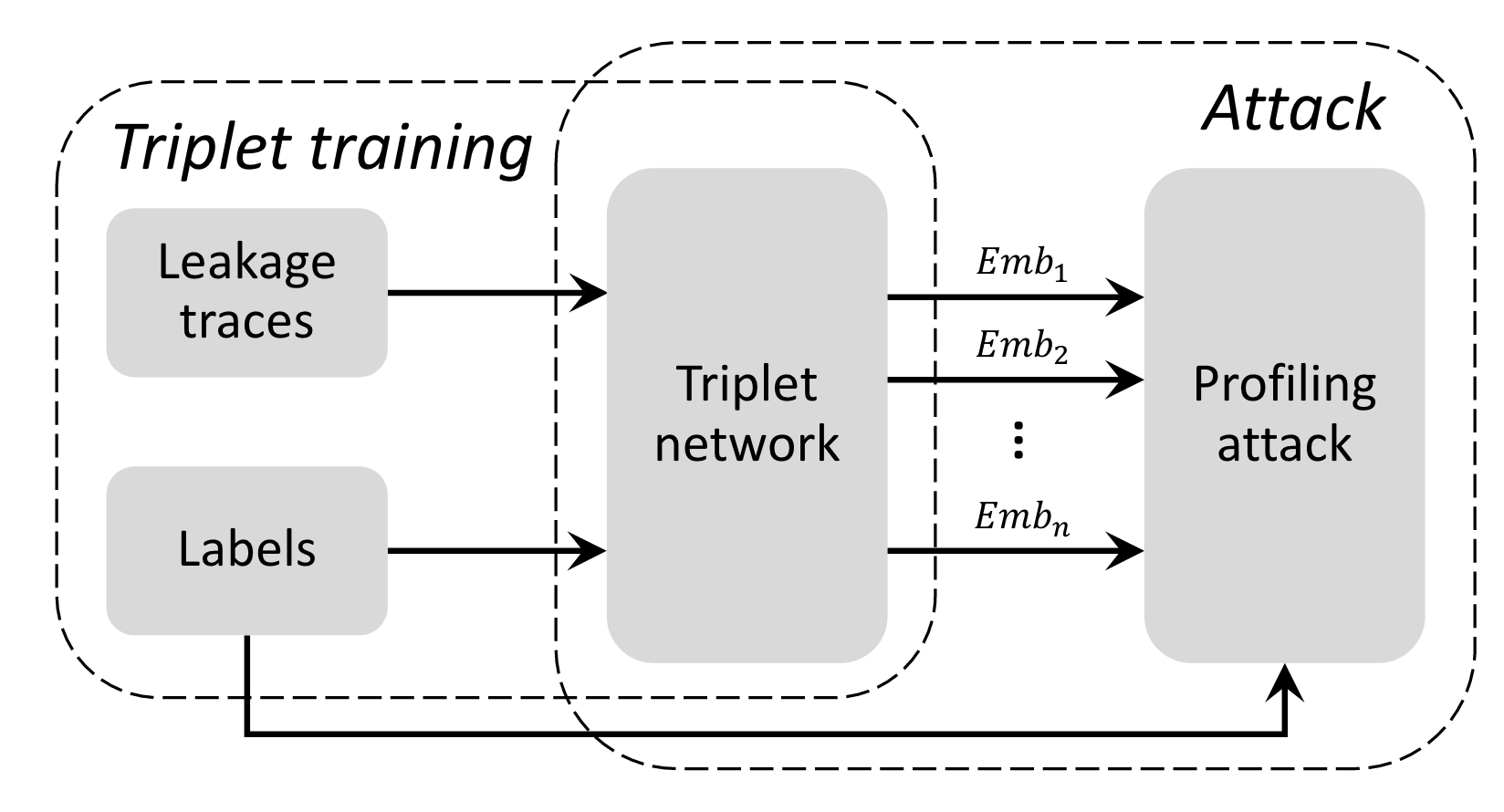
攻击步骤

  1. 训练三元组网络，获取Embeddings
  2. 使用训练好的Embeddings来完成攻击
攻击流程 三元组神经网络超参数搜索空间 详细参数

实验结果

ASCAD_F、ASCAD_R、AES_HD攻击结果

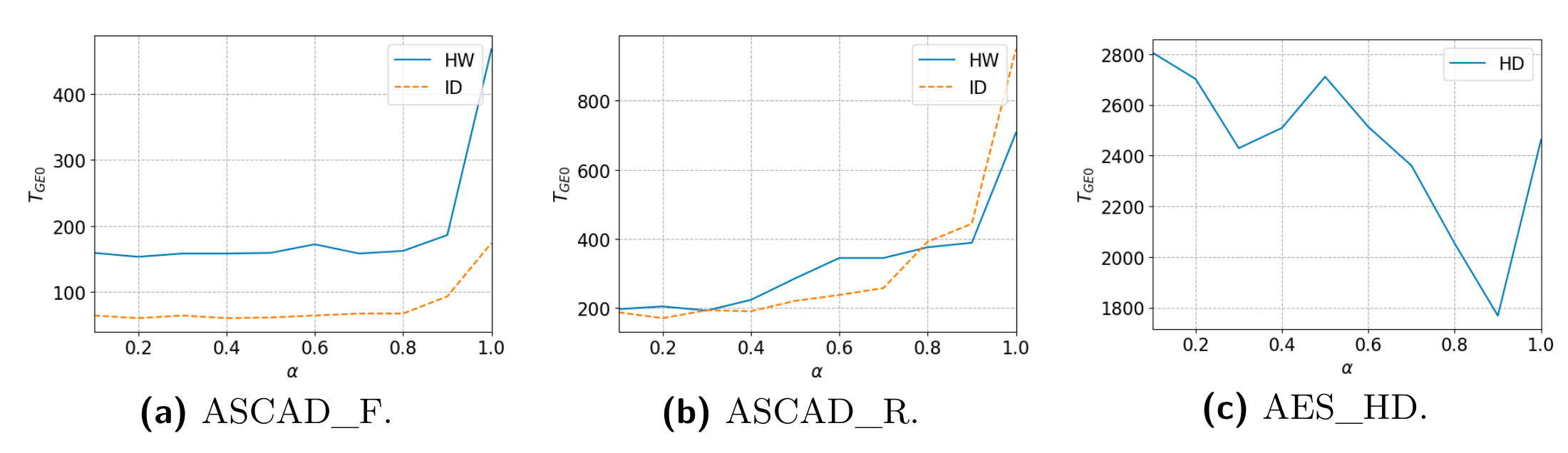
这里是HW/ID两个泄露模型的猜测熵

去同步数据集ASCAD_F上攻击效果（level=50、100） 去同步数据集ASCAD_R上攻击效果（level=50、100） 去同步数据集AES_HD上攻击效果（level=50、100）

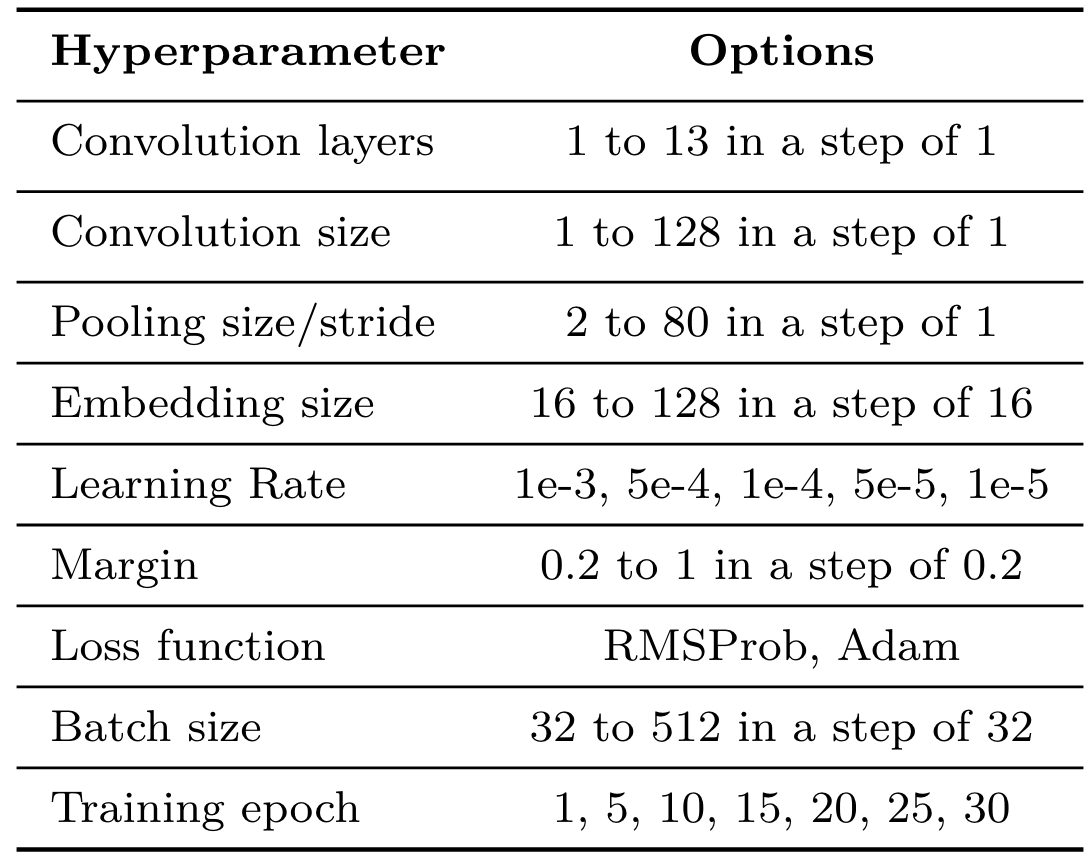
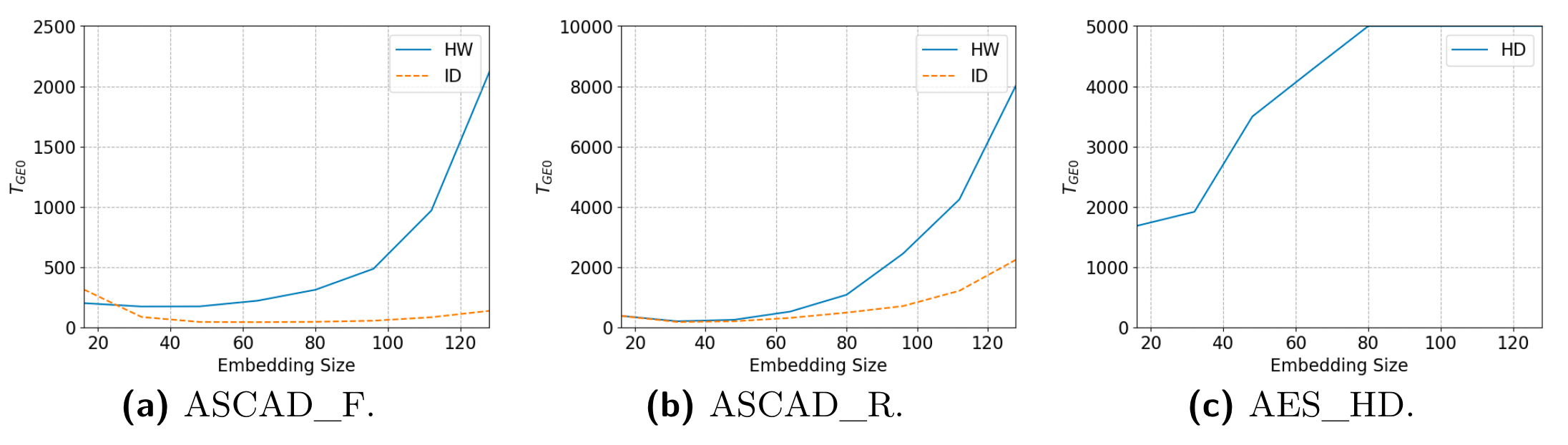
验证aa超参对收敛到0所需要的能量迹数量的影响

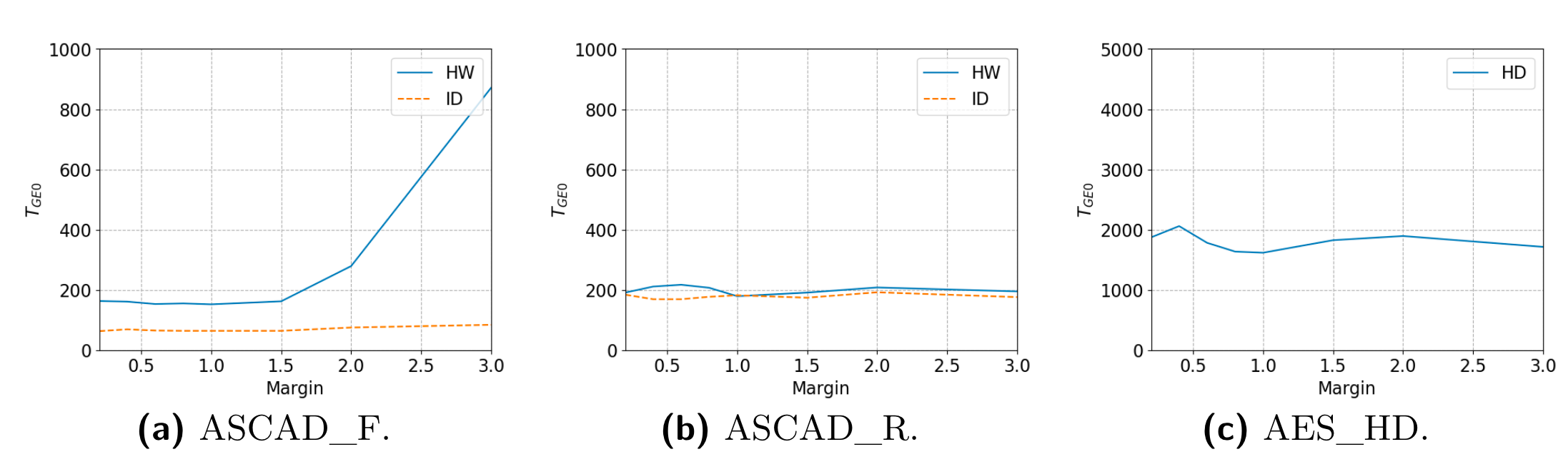
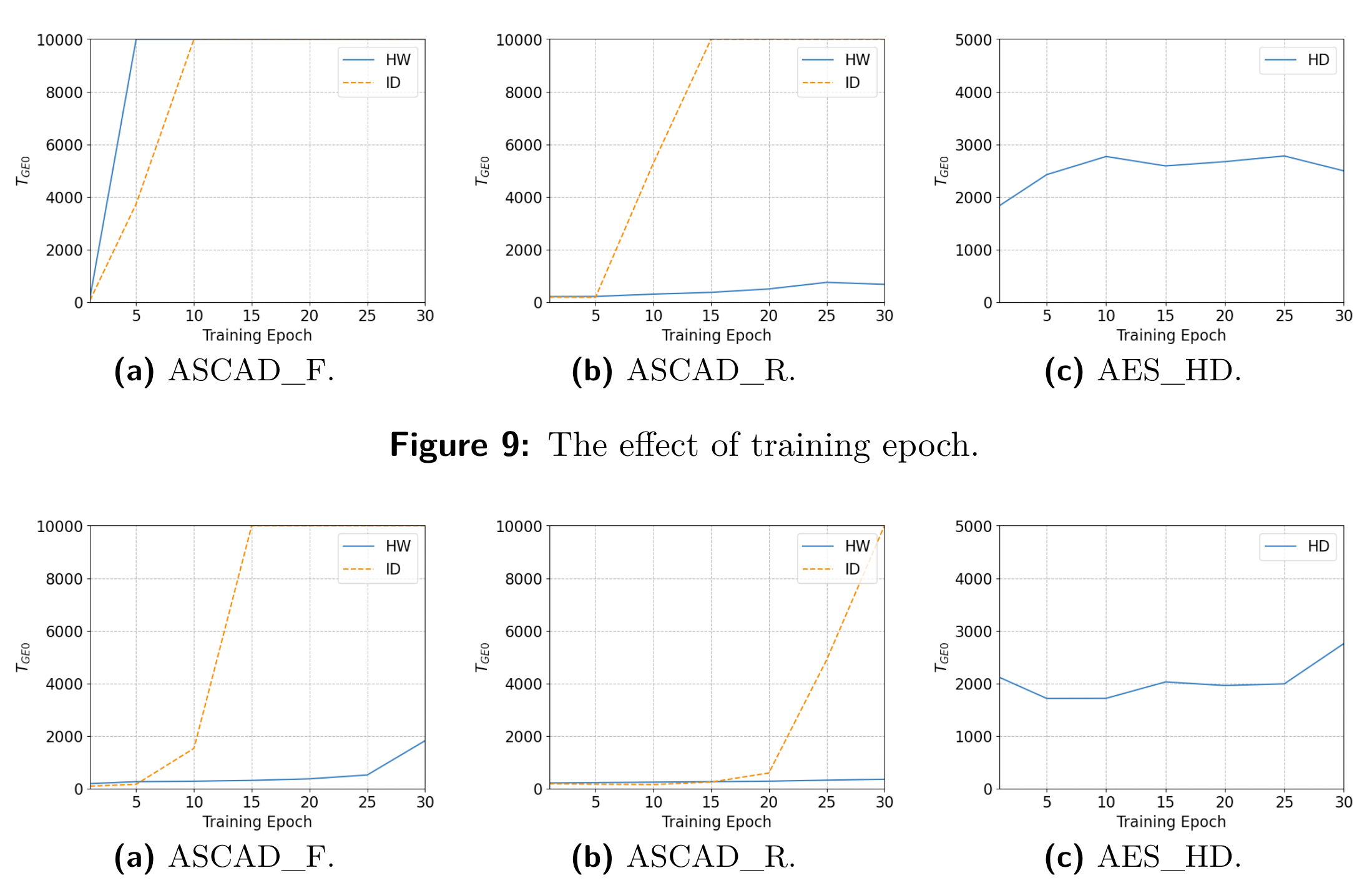
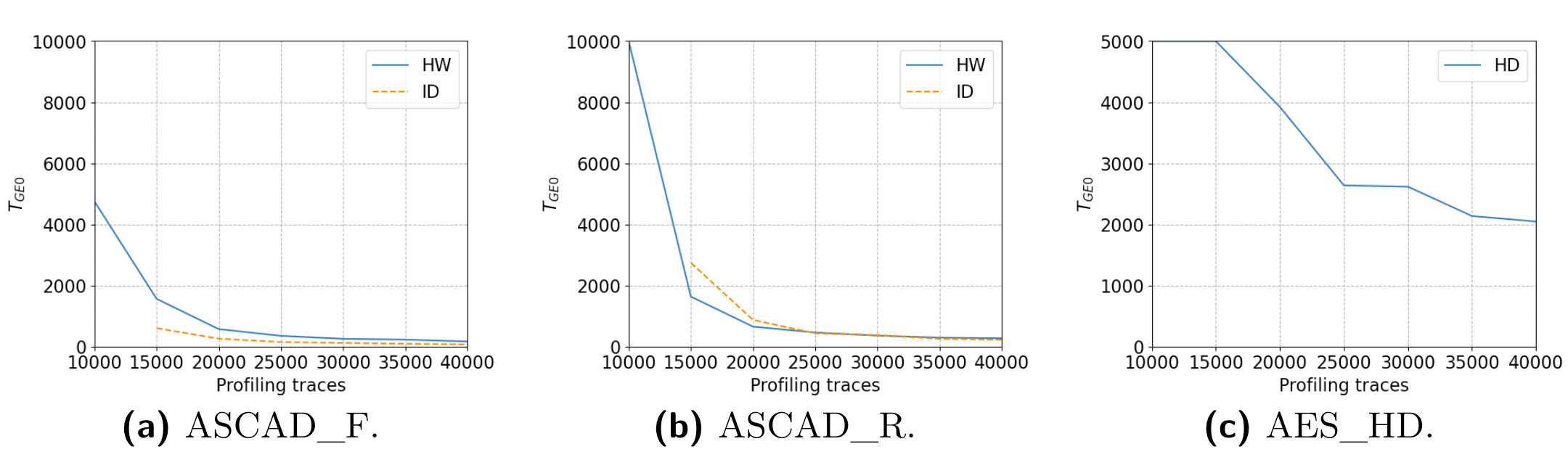
阿尔法超参影响 不同Embeddings大小对数攻击效果的影响 margin对攻击效果的影响 不同Epoch对攻击效果的影响 训练集大小对猜测熵的影响

总结

作者基于原始三元组模型提出了一个新的基于混合距离的三元组模型，后续可以拼接到其他需要对抗时钟抖动等下游任务中。