文章信息

  • 作者：Guilherme Perin, Lichao Wu and Stjepan Picek

  • 单位：Leiden Institute of Advanced Computer Science (LIACS), Leiden University, Niels Bohrweg 1, 2333 CA Leiden, The Netherlands;Faculty of Electrical Engineering, Mathematics & Computer Science, Delft University of Technology, Mekelweg 5, 2628 CD Delft, The Netherlands; Digital Security Group, Radboud University, Houtlaan 4, 6525 XZ Nijmegen, The Netherlands

  • 出处：algorithms

  • 标题：The Need for Speed: A Fast Guessing Entropy Calculation for Deep Learning-Based SCA

  • 日期：2023年2月23日

背景

目前，侧信道攻击研究者们为了缩短训练所需时长，通常采用减小模型容量或者缩小训练集等方法，但此类方法会影响模型的泛化性能以及可学习性。ES（early stopping）作为一种有效监控模型训练以及防止过拟合的方案，它通过监控模型的损失值来完成对模型性能的监控，而在侧信道攻击中，模型的性能与损失值并没有绝对的对应关系。猜测熵作为侧信道攻击常用评估方案，使用猜测熵来作为ES的指标是可行的，但是由于计算猜测熵所需的时间开销过大，因此在超参数搜索时往往会导致搜索时间过长，在极端的情况下是不可行的。

内容

相关工作

Zhang等人[1]提出了一种猜测熵估计算法GEEA，缩短了计算猜测熵的时间，Perin等人[2]利用互信息方法来检测模型训练在某个Epoch时的性能。

主要工作

在每个Epoch结束后快速计算一次猜测熵FGE，通过判断猜测熵在哪个epoch最小。

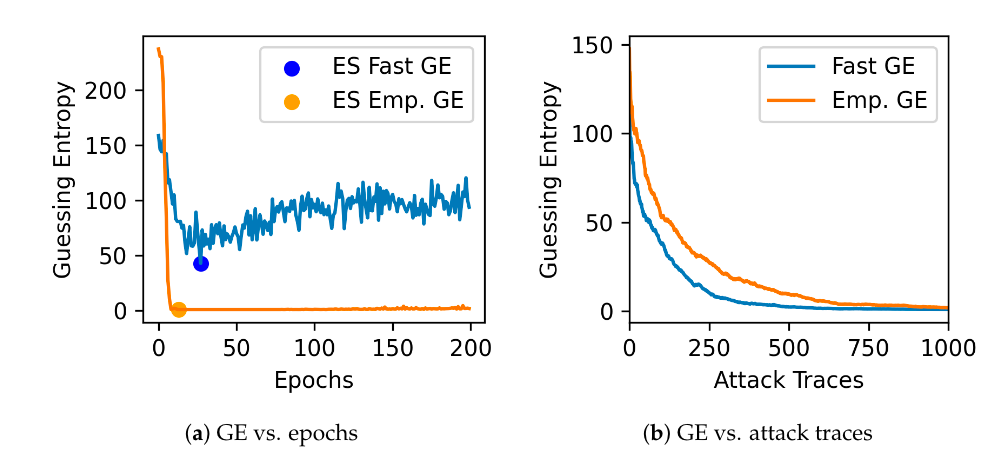
流程 FGE与GE的结果

可以看到使用FGE作为指标的模型猜测熵收敛到1的速度更快。

FGE关键代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# guessing entropy and success rate
def fast_ge(runs, nt_kr, model, x_attack, labels_key_hypothesis, correct_key, leakage_model):
    start_time = time.time()
    nt = len(x_attack)

    # -----------------------#
    # predict output probabilities for shuffled test or validation set
    # -----------------------#
    output_probabilities = np.log(model.predict(x_attack) + 1e-36)
    key_ranking_sum = 0
    if leakage_model == "HW":
        probabilities_kg_all_traces = np.choose(labels_key_hypothesis, output_probabilities.T).T
    else:
        probabilities_kg_all_traces = np.zeros((nt, 256))
        for index in range(nt):
            probabilities_kg_all_traces[index] = output_probabilities[index][
                np.asarray([int(leakage[index]) for leakage in labels_key_hypothesis[:]])
            ]

    # ------------------------#
    # run key rank "runs" times and average results.
    # ------------------------#
    for run in range(runs):
        r = np.random.choice(range(nt), nt_kr, replace=False)
        probabilities_kg_all_traces_shuffled = probabilities_kg_all_traces[r]
        key_probabilities = np.sum(probabilities_kg_all_traces_shuffled[:nt_kr], axis=0)
        key_probabilities_sorted = np.argsort(key_probabilities)[::-1]
        key_ranking_sum += list(key_probabilities_sorted).index(correct_key) + 1

    guessing_entropy = key_ranking_sum / runs
    print("GE = {}".format(guessing_entropy))

    return guessing_entropy, time.time() - start_time

这里贴出来mlscat计算猜测熵源码

1
2
3
4
5
6
7
8
9
10
11
12
def rank(predictions, num_traces, targets, key, interval=1):
    rank_time = np.zeros(int(num_traces/interval))
    pred = np.zeros(256)
    idx = np.random.randint(predictions.shape[0], size=num_traces)
    for i, p in enumerate(idx):
        for k in range(predictions.shape[1]): #256
            pred[k] += predictions[p, targets[p, k]]
        
        if i % interval == 0:
            ranked = np.argsort(pred)[::-1]
            rank_time[int(i/interval)] = list(ranked).index(key)
    return rank_time

fast_ge在拿到predictions后直接对其做了映射，假设密钥$$k_i=1$$，对应的$$predictions_i[1]$$就是该密钥的预测概率，也就是位置与密钥值相等，在下方for循环中计算概率和时直接进行了累加，最后取排名均值。

代码看不出有什么区别，最后在传参处发现

1
2
3
4
5
6
callback_fast_ge = Callback_EarlyStopping(number_of_traces_key_rank,X_validation_reshape[:validation_traces_fast],labels_key_hypothesis[:, :validation_traces_fast], correct_key, leakage_model)
callback_slow_ge = 
Callback_EarlyStopping(validation_traces, X_validation_reshape, labels_key_hypothesis, correct_key,
                                                  leakage_model)

#validation_traces_fast = 500

这里fastge传的是500个。

总体的方法就是这样，少量验证集完成猜测熵的快速计算。

接下来作者采用贝叶斯优化（BO）配合ES来完成超参数搜索，BO在keras库里有。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
script_bo_fge.py

    tuner = BayesianOptimization(build_cnn_model,
                                 objective=kt.Objective(objective, direction=direction),
                                 max_trials=max_id,
                                 executions_per_trial=1,
                                 directory=save_folder_bo,
                                 project_name=project_folder,
                                 overwrite=True)
    # tuner.on_epoch_end()

    tuner.search_space_summary()
    tuner.search(x=X_profiling_reshape,
                 y=Y_profiling,
                 epochs=epochs,
                 batch_size=batch_size,
                 validation_data=(X_validation_reshape[:validation_traces_fast], Y_validation[:validation_traces_fast]),
                 verbose=2,
                 callbacks=[callback_early_stopping])
    tuner.results_summary()

数据集

黑盒

名称 链接
ASCAD https://github.com/ANSSI-FR/ASCAD
CHESCTF 2018 https://chesctf.riscure.com/2018/content?show=training

模型架构

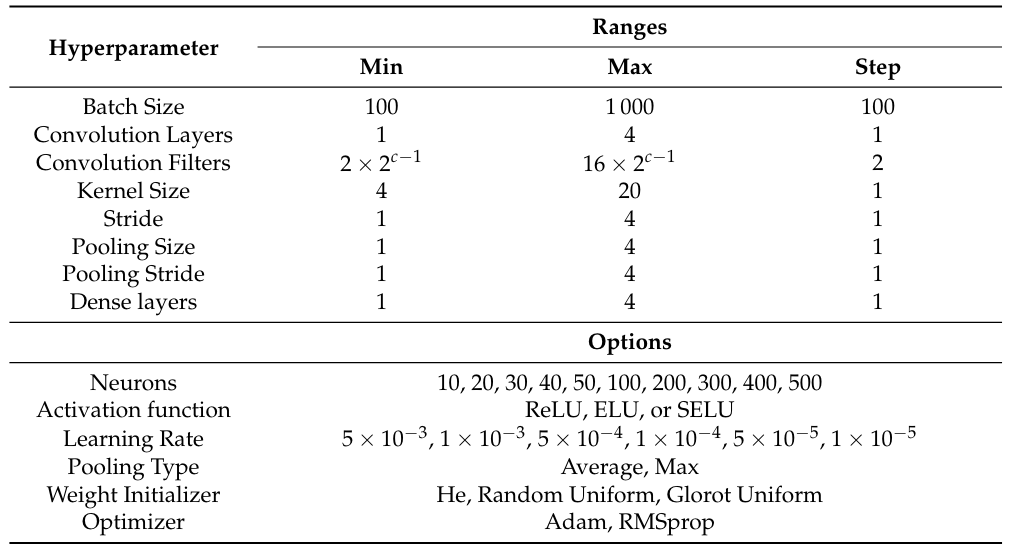
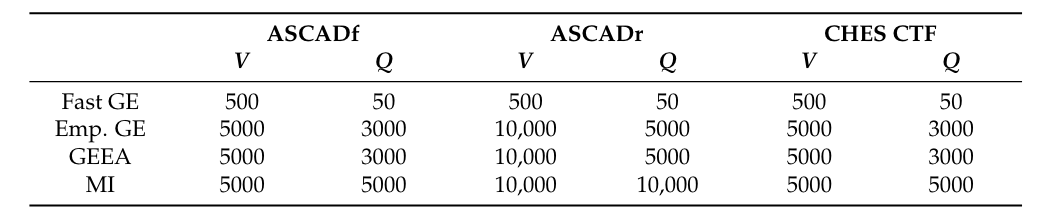
模型架构以及超参数组合图 不同数据集上不同方案所需验证集数量

结果

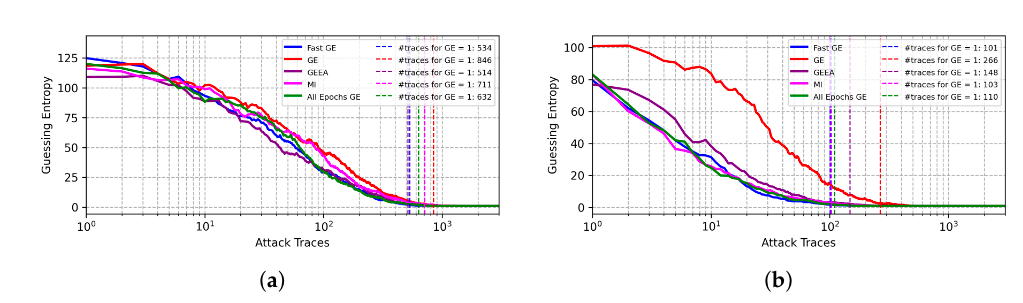
ASCADf数据集上汉明重量（左）以及身份泄露模型猜测熵收敛曲线

在ASCAD数据集上，采用身份泄露模型，FGE方案需要101条能量迹可将猜测熵收敛为1。

这里主要看BO+FGE，在身份泄露模型下，ASCADf数据集上需要72条即可收敛，汉明重量模型需要455条。

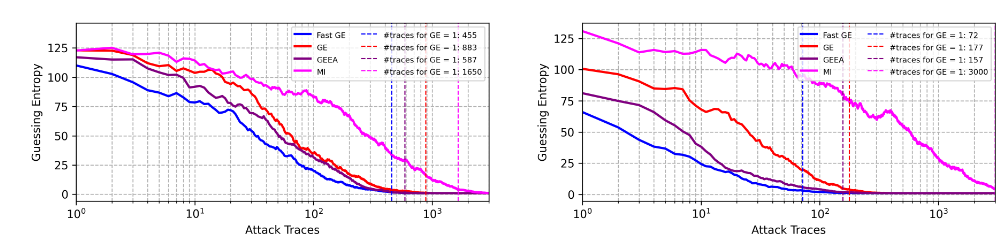
ASCADf BO&FGE 猜测熵收敛曲线

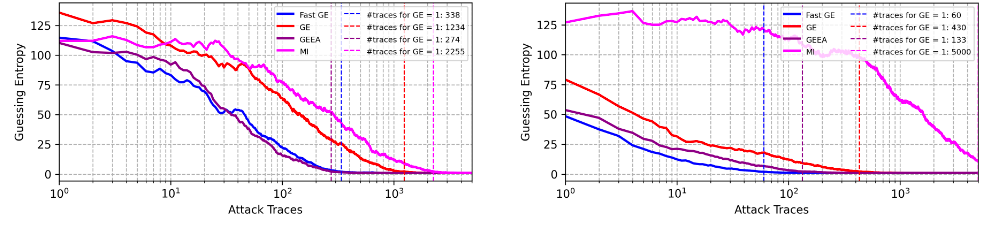
而在ASCADr数据集上，身份泄露模型仅需60条即可收敛。

ASCADr

  1. Zhang, J.; Zheng, M.; Nan, J.; Hu, H.; Yu, N. A Novel Evaluation Metric for Deep Learning-Based Side Channel Analysis and Its Extended Application to Imbalanced Data. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2020 , 2020 , 73–96 ↩︎

  2. Perin, G.; Chmielewski, L.; Picek, S. Strength in Numbers: Improving Generalization with Ensembles in Machine Learning-based Profiled Side-channel Analysis. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2020 , 2020 , 337–364 ↩︎