文章信息

  • 作者：Libang Zhang , Xinpeng Xing , Member, IEEE, Junfeng Fan, Member, IEEE, Zongyue Wang, and Suying Wang

  • 单位：-

  • 出处：IEEE TRANSACTIONS ON COMPUTER-AIDED DESIGN OF INTEGRATED CIRCUITS AND SYSTEMS

  • 标题：Multilabel Deep Learning-Based Side-Channel Attack

文章内容

背景

近年来，将深度学习应用在侧信道攻击中的研究越来越多，特别是在模板攻击、泄露评估等方面，在 Study of Deep Learning Techniques for Side-Channel Analysis and Introduction to ASCAD Database 那篇文章中，采用MLP、CNN模型对在设备上采集到的能量迹作分析，给出了指导性的超参数。在本论文中提到Lerman等人[1]首次使用SVM去分析3DES的密钥，成功分析单个比特密钥，并通过相同操作遍历来恢复整个密钥。Zaid等人[2] 引入权重可视化和热图来对泄露进行分析，并提出了一种根据去同步程度生成CNN架构的方法，本文作者在实验结果处主要与Z等人的结果做了对比。最后Perin[3]等人提出一种在SCA中使用集成学习的方法，对应在本文中是由几个弱分类器集成为单个强分类器。

作者做了什么

  1. 在DL-SCA中提出了多标签分类这种概念
  2. 将提出的方法应用到了ASCAD数据库的几种类别
  3. 给出了nn模型的结构

技术

侧信道攻击

将侧信道攻击划分为非建模侧信道攻击和建模侧信道攻击两种，对于非建模侧信道攻击，假设攻击者只能收集到目标设备的信息；而对于建模侧信道攻击，假设攻击者拥有与被目标设备相同的副本设备，可以事先对副本设备进行泄露采集分析，从而对被目标设备进行攻击。本文中针对后一种方法进行研究。

建模侧信道攻击

建模侧信道分建模阶段和攻击阶段，在深度学习中与之相对应的是训练阶段和测试阶段。

建模阶段

在建模阶段攻击者建立数据集Dtrain={(Xi,Yi)∣i=1,2,...,Nt}D_{train} = \{(X_i, Y_i)|i = 1, 2, ..., N_t\},其中XiX_i代表第i条能量迹，YiY_i表示对应的标签,总共有NtN_t对, 这里攻击者知道对应加密密钥KiK_i,明文PiP_i,密文CiC_i,通过建立泄露模型Vi=L(Ki,Pi,Ci)V_i=L(K_i,P_i,C_i)来计算泄露的数据,通过应用功率模型表示Yi=φ(Vi)Y_i = \varphi(V_i),通过一个估计模型即函数f(X,P,C)f(X,P,C)来表示训练集。

攻击阶段

攻击者通过对函数f(X,P,C)f(X,P,C)以及泄露模型LL和功率模型φ\varphi来预测正确的密钥, 本文介绍这方面时这里作者写的有一点歧义,他写的在目标设备上基于已知的明文和密文,以及要攻击的能量迹来推测出密钥,已知被攻击的设备明文密文了还推测密钥

深度学习

相较于机器学习,深度学习采取NN(神经网络)的形式,即通过堆叠多个神经层,神经层中包含多个神经元来表面上模拟人脑工作机制,早期的ML模型为多层感知机模型(Multilayer Perceptron, MLP),以及目前在DL-SCA中广泛应用改进的卷积神经网络模型(Convolutional Neural Network, CNN).

MLP

MLP是线性分类模型,主要用来做二分类任务,将结果一分为二,阳性为1,阴性为-1,其工作形式可以用公式y=sign(w⋅x+b)y=sign(w\cdot x + b)来表示,sign只表示一种方法,即复合函数

sign(x)={1,x≥0,−1,x<0,sign(x)= \left\{ \begin{array}{ll} 1,&x \ge 0,\\ -1,&x < 0, \end{array} \right.

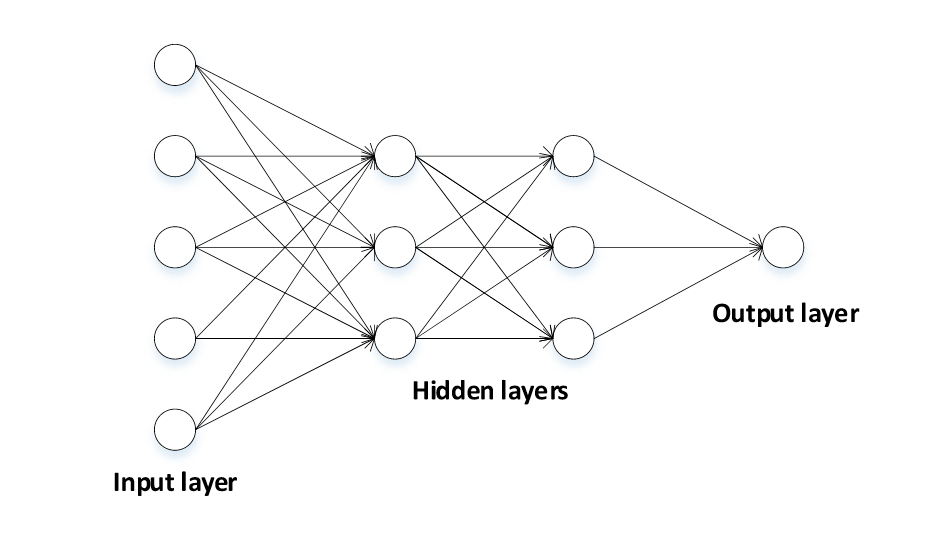
单层的MLP模型不能用来解决异或问题,之后研究者通过增加模型的层数,更换激活函数来弥补这方面的不足,例如现在用的比较多的sigmoid,每一层的输出都对应下一层的输入,每个神经元都与最后一层的所有神经元有关,模型经典架构如图1所示,但往往层数的增多会导致计算复杂度越来越高.

图1 经典多层感知机模型

CNN

CNN引入卷积池化层来解决计算复杂度过高等问题,详细架构以及具体实现在卷积神经网络(CNN)中, 这里CNN在处理一维数据时公式如下.

z[I]=∑k=1mw[k]⋅x[i−k+1]z[I] = \sum\limits_{k=1}^{m}w[k]\cdot x[i-k+1]

多分类与多标签分类

在看这篇文章的关键技术前,需要搞懂什么叫多分类与多标签分类.举一个例子

instance a b c d e
x1 1 0 0 0 0
x2 0 1 0 0 0
x3 0 0 1 0 0
x4 0 0 0 1 0
x5 0 0 0 0 1

A,b,c,d,e这属于一个互斥的类,即有a不能有b,换言之五首歌曲,abcde就是歌曲的名称,这就叫做多分类,而对于多标签,就上边的歌曲而言,每首歌都对应一个或多个标签,所有的标签并不全都互斥,这样的分类即为多标签分类,采用深度学习的方法,训练时最后FN设置4个输出节点,激活函数用sigmoid作二分类,判断是否属于该标签.

instance 华语 情歌 古典 摇滚 民谣
x1 1 1 1 0 0
x2 1 1 0 0 1
x3 1 0 1 0 0
x4 1 0 0 1 0
x5 1 0 1 0 1

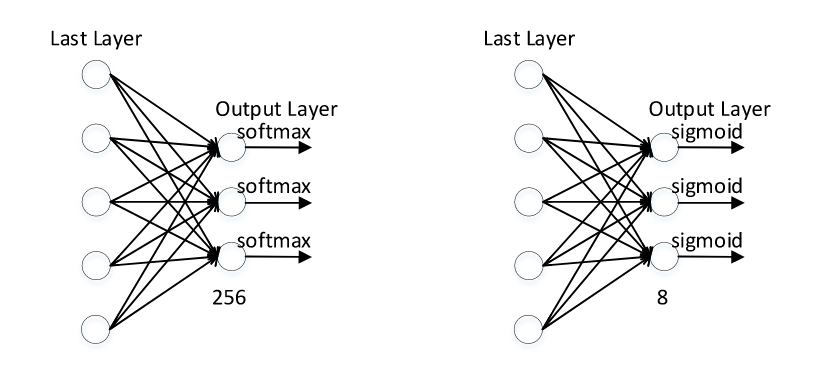
作者给出多标签分类的具体细节,初始时给每条能量迹打上八个标签,每一个标签都做二分类,0或1来表示特定的bit位,8个标签组成1byte密钥数据,这样FN层就仅需要8个神经元,大大减少了最后的分类复杂度,在单比特分类任务中,由于AES的S盒为8bit,即共有282^8种可能,最后密钥每一个比特都对应256种可能,二者网络结构对比如图2所示.

图2 左侧为单比特模型输出层,右侧为多标签分类模型的输出层

k~=arg⁡max⁡k∏i=1NaP(K=k∣Xi)=arg⁡max⁡k∑i=1Nalog(P(K=k∣Xi))=arg⁡max⁡k∑i=1Nalog(P(Vi=vi∣Xi))s.t.L(k,pi,ci)=vi,i=1,2,...,Na=arg⁡max⁡k∑i=1Na∑j=18log(P(Yi[j]=yi[j]∣Xi))s.t.L(k,pi,ci)=yi,i=1,2,...,Na.\begin{aligned} \tilde{k} &= \mathop{\arg\max}\limits_{k}\prod\limits_{i=1}^{N_a}P(K=k|X_i) \\ &= \mathop{\arg\max}\limits_{k}\sum\limits_{i=1}^{N_a}log(P(K=k|X_i))\\ &= \mathop{\arg\max}\limits_k\sum\limits_{i=1}^{N_a}log(P(V_i=v_i|X_i))\\ s.t. \mathit{L(k,p_i,c_i)=v_i, i=1,2,...,N_a} \\ &= \mathop{\arg\max}\limits_{k}\sum\limits_{i=1}^{N_a}\sum\limits_{j=1}^{8}log(P(Y_i[j]=y_i[j]|X_i))\\ s.t. \mathit{L(k,p_i,c_i)=y_i, i=1,2,...,N_a}. \end{aligned}

由公式可以看出每条能量迹上累加了8次,Y是label,$$Y_i=\varphi(V_i)=\varphi(L(K_i,P_i,C_i))$$,L就是泄露模型, ϕ\phi是功耗模型

实验数据与结果对比

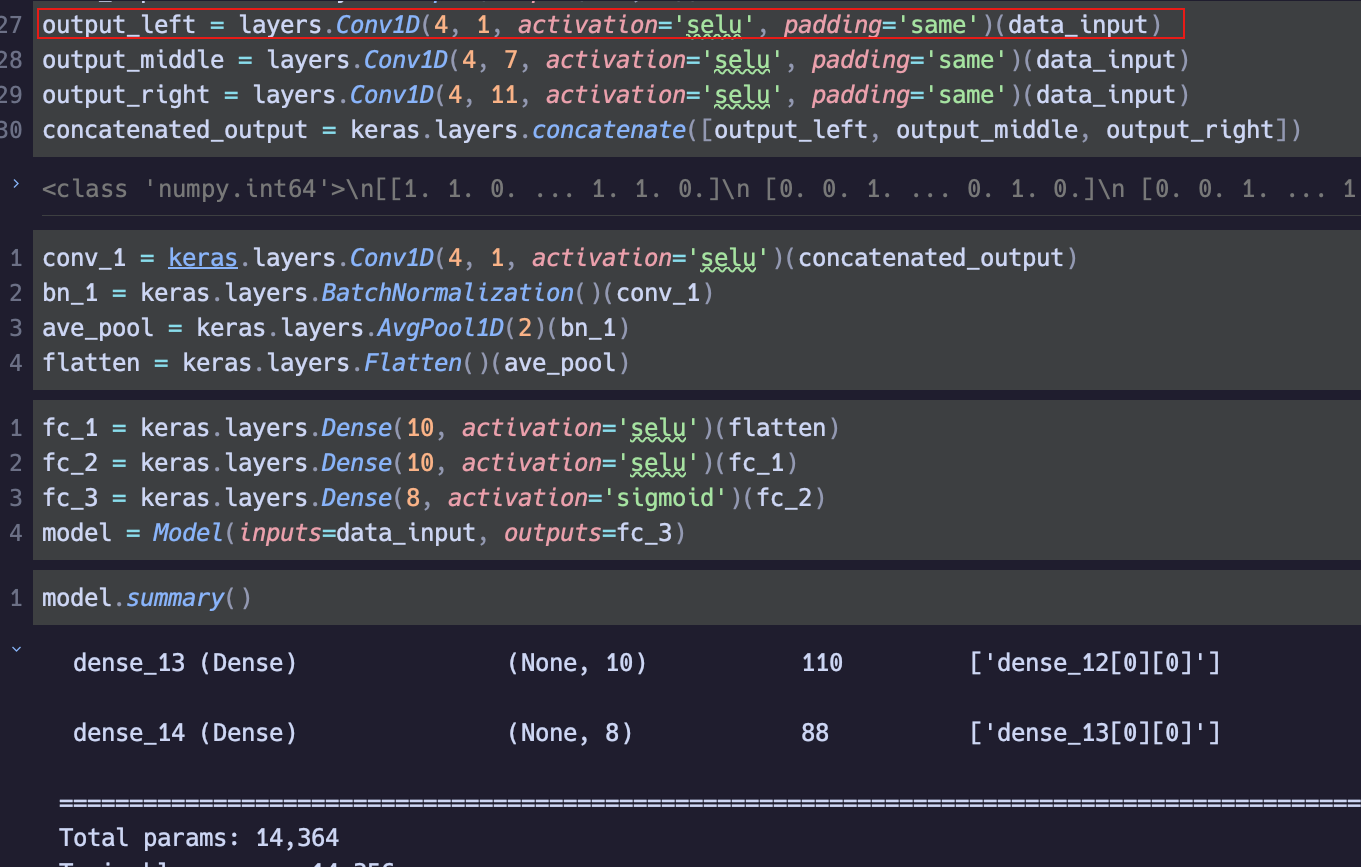
采用猜测熵来评估SCA攻击效率,猜测熵即猜对正确密钥所需要的次数,通常为1时被视作猜测成功,作者随机了一百次之后取平均的猜测熵(这个操作目前还没实现过所以具体不太理解,这两天跑一下,作者采用inception的思想,设计的神经网络架构如表1所示。

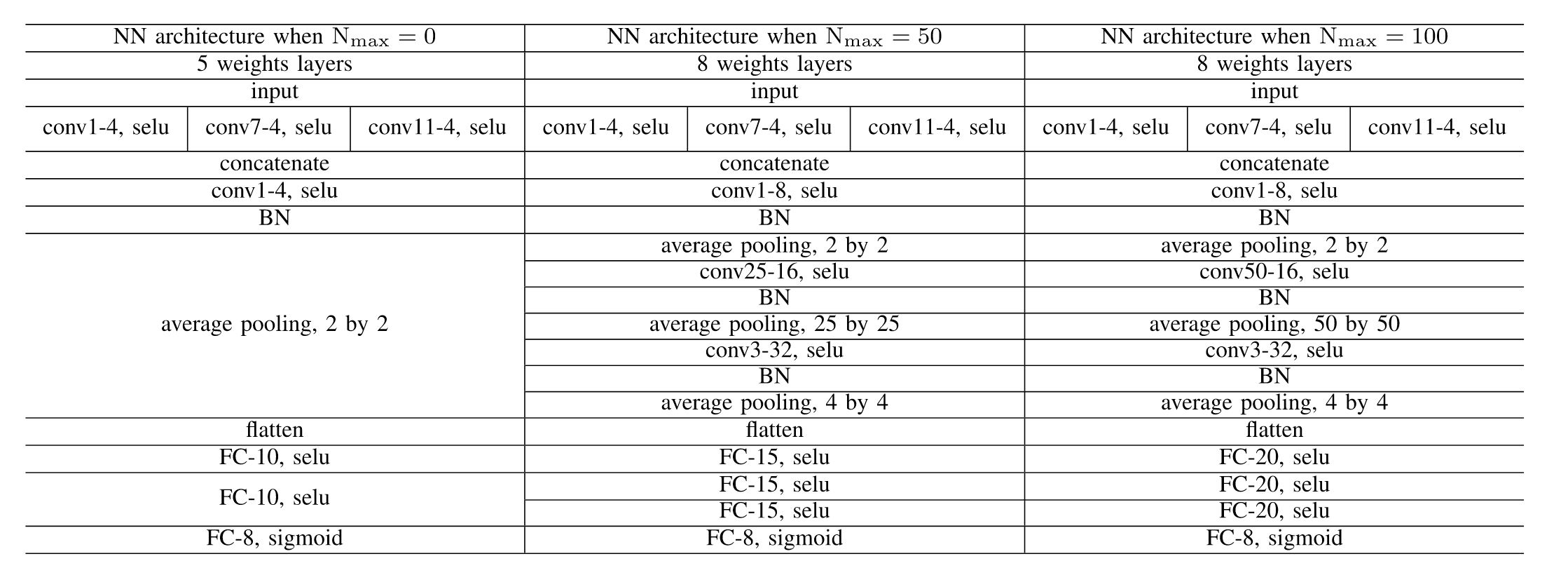
表1 神经网络架构

作者说第一个大小为1的卷积核是为了减小复杂度,他并没有跟大小为7的卷积核串行运算,怎么会减小后边的复杂度?因为在inception中,他是通过串行计算时利用1x1的卷积核减小第三个维度来降低复杂度的。测试了一下,如图1,图2所示.

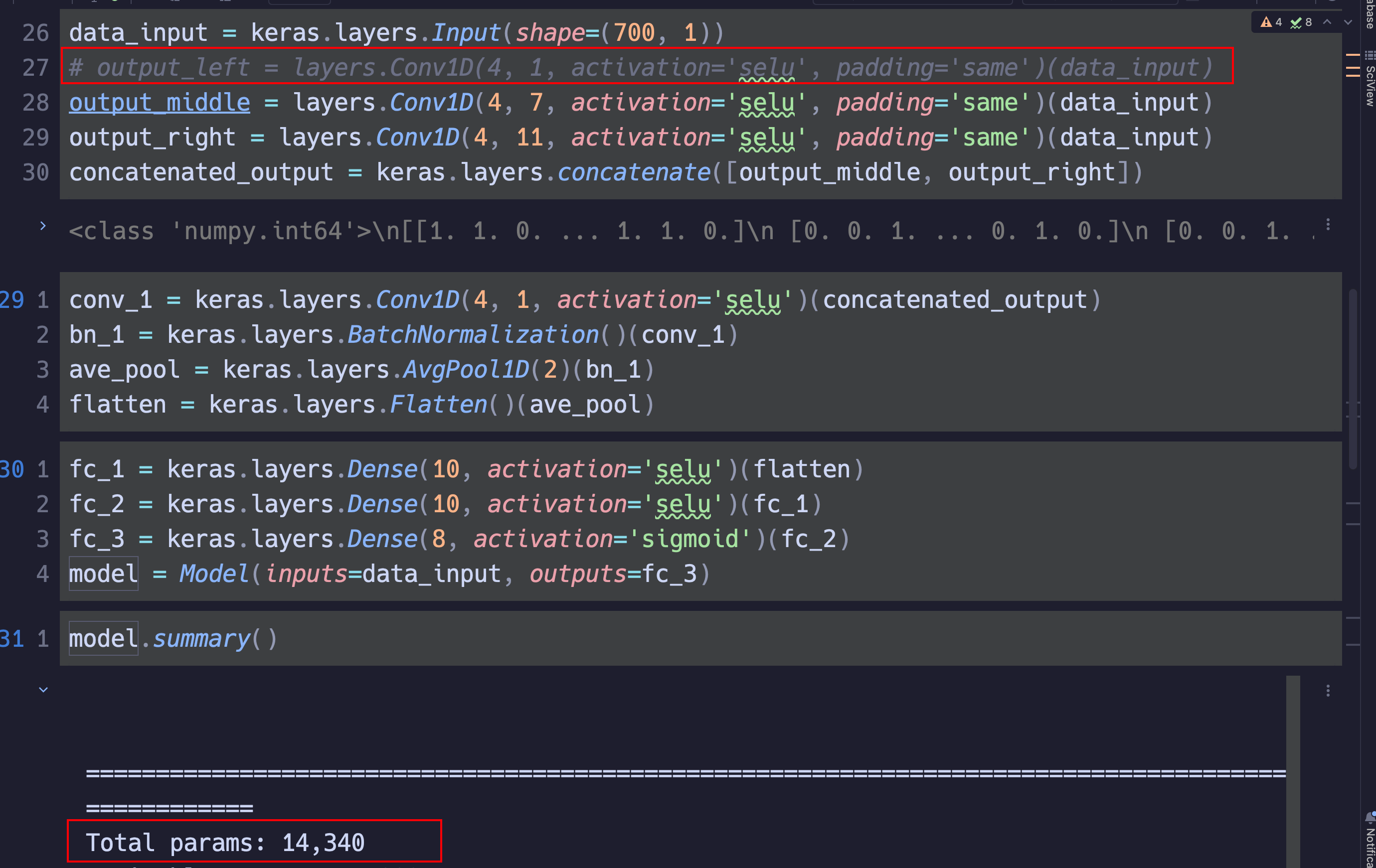
图1 去掉大小为1的卷积核后的复杂度

结果1

图2 带有大小为1卷积核的复杂度

结果2

结果

ASCAD
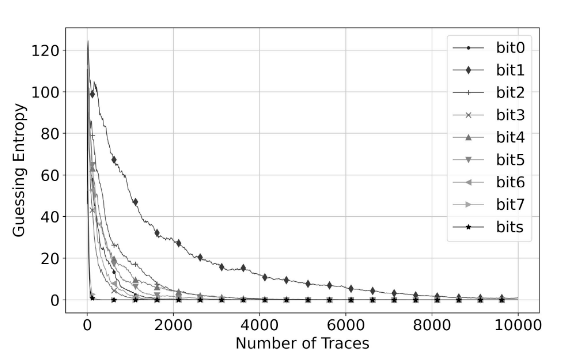
图3 N=0时攻击结果 表2 对比

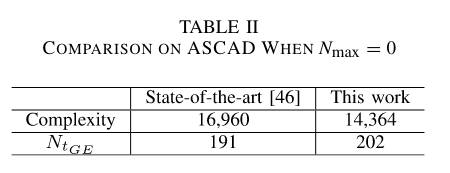
在未加入时钟抖动的ASCAD数据集中, 可以看到本文的工作与文献46[4]在复杂度略微减小但GE=1时所需的能量迹条数是相差不大的。

但在随机时钟抖动的数据集中,本文的结果要优于前人的工作,如表3,表4所示。

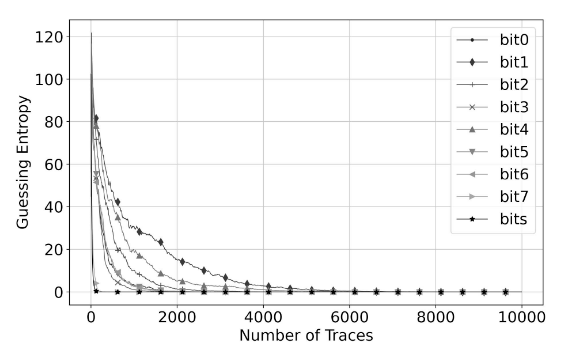
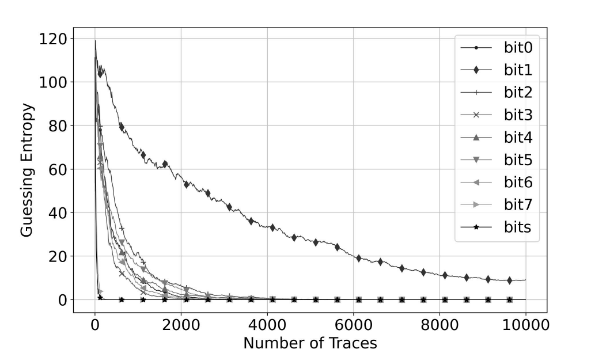
图4 加入随机延迟max为50的随机时钟抖动攻击结果 表3 对比 图5 加入随机延迟max为100的时钟抖动攻击结果 表4 对比

可以看出,利用卷积的方法针对于不对齐能量迹的攻击结果较好。

AES_HD
图6 针对AES_HD数据集的NN架构

可以看到,到这架构就相对于比较简单,两个一维卷积核用来降低复杂度, (这个效果待定,是否降低了参数量还需要做实验我目前还没写到会在实现那里补上),之后经过一个平均池化,池化窗口跟步长都是2,最后展平在经过两个全连接层,最后经过激活函数sigmoid来进行分类输出,可以看到相较于之前的工作成果在复杂度以及GE上有较好的提升,结果如图7,表5所示。

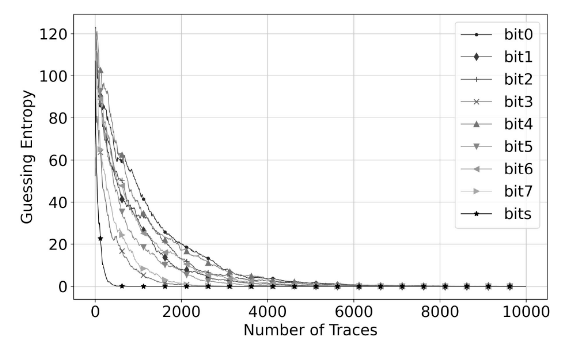
图7 AES_HD数据集攻击结果 表5 对比结果
AES_RD
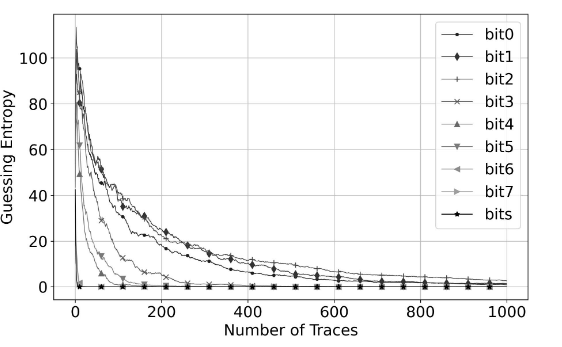
图8 AES_RD对应NN架构 图9 攻击结果 表6 对比结果

这个效果并不是太好,虽然减少了复杂度,但是增大了GE。

总结

作者提出了一种多标签分类的方法针对AES算法来进行攻击,实验的结果表明,在加入时钟抖动后的攻击效果提升较大,且与之前的多分类模型的攻击模型相比复杂度有所降低。

PS：2024.4.5，计算多标签的猜测熵耗费的时间很多，目前我还没找到一个快速转化的方法。

  1. L. Lerman, G. Bontempi, and O. Markowitch, Side Channel Attack: An Approach Based on Machine Learning, Center Adv. Security Res. Darmstadt, Darmstadt, Germany, 2011. ↩︎

  2. G. Zaid, L. Bossuet, A. Habrard, and A. Venelli, “Methodology for efficient cnn architectures in profiling attacks,” IACR Trans. Cryptograph. Hardw. Embedded Syst., vol. 2020, no. 1, pp. 1–36, Nov. 2019. [Online]. Available: https://tches.iacr.org/index.php/TCHES/article/view/8391 ↩︎

  3. G. Perin, “Deep learning model generalization in side-channel analysis,” in Proc. IACR Cryptol. ePrint Archive, 2019, p. 978. ↩︎

  4. G. Zaid, L. Bossuet, A. Habrard, and A. Venelli, “Methodology for efficient cnn architectures in profiling attacks,” IACR Trans. Cryptograph. Hardw. Embedded Syst., vol. 2020, no. 1, pp. 1–36, Nov. 2019. [Online]. Available: https://tches.iacr.org/index.php/TCHES/article/view/8391 ↩︎