文献阅读笔记-Label Correlation in Deep Learning-Based Side-Channel Analysis
文章信息
-
作者:Lichao Wu1, Léo Weissbart1,2, Marina Krcˇek1 , Huimin Li1, Guilherme Perin1,2, Lejla Batina2, and Stjepan Picek1,2
-
单位:
-
The Faculty of Electrical Engineering, Mathematics and Computer Science, Delft University of Technology, 2628 XE Delft, The Netherlands
-
The Digital Security Group, Radboud University, 6525 EC Nijmegen, The Netherlands.
-
-
期刊: IEEE Transactions on Information Forensics and Security
文章内容
相关知识
描述程度(description degree)
标签分布学习的核心概念,给定输入$x$,则$d^{y_i}_{x}$代表标签$y_i$被选中的概率,所有可能的标签概率和为1,如公式1所示。
更形象的说,假设一张图里有草、松鼠、石头,人们第一眼往往会认为这是一张松鼠的图片,很会说这是一张关于石头、草地的照片,也就是说,相较于草和石头,松鼠这个标签对于这张图的Description degree更高。具体分布如图表1所示。
在本文中,通过信噪比来挑选两个兴趣点,POI1设置为x,POI2设置为y,绘制不同类对应的坐标;此外,对于HW泄露模型,采用One-Hot编码构造以及对HW进行分布式标签描述。结果如图2所示。
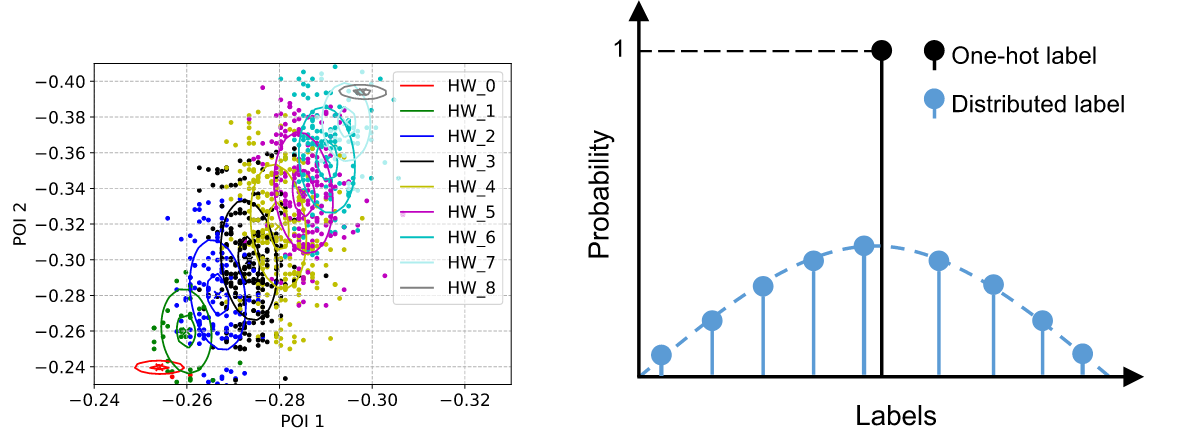
标签分布学习
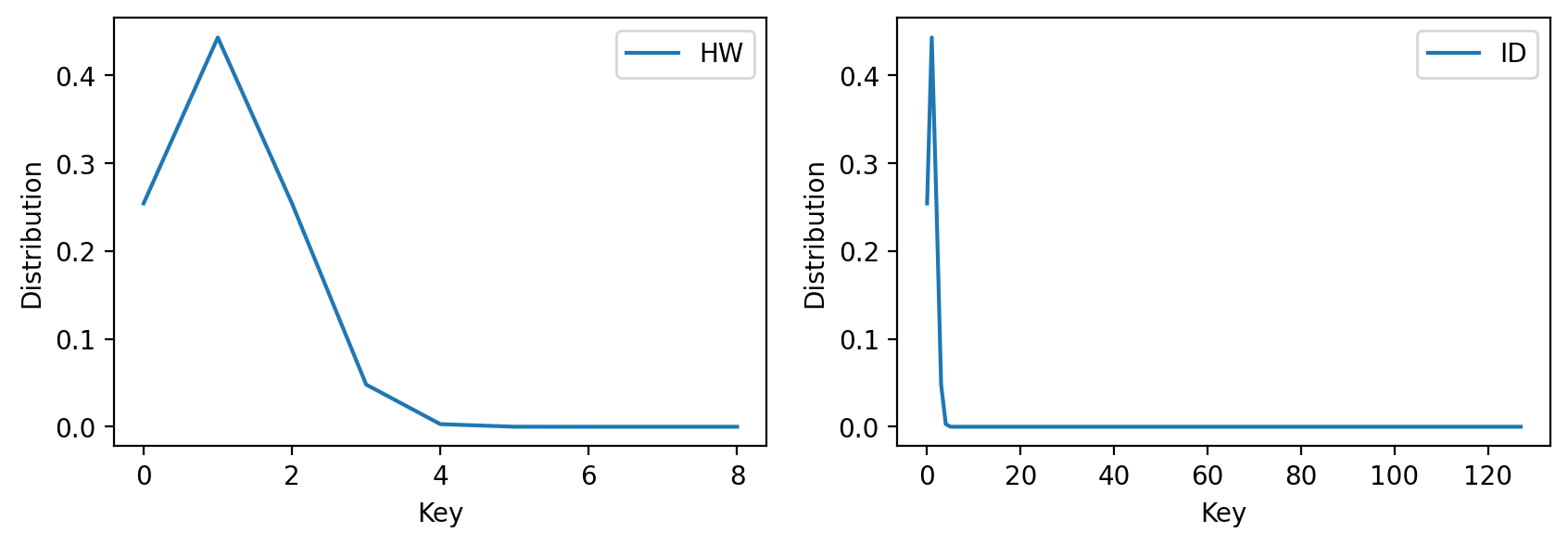
令训练集中的样本标签对表示为$T(x, y)$,此时的目标是学习一个函数$f^{\theta}_M$以预测标签$\hat{y}$,这里分布式标签表示为$D(y)$,具体构造方法如公式2所示:
假设当前标签为1,则标签分布结果如下图所示。
皮尔逊相关性和斯皮尔曼相关性
给定两变量$X、Y$,此时有$n$对观测值。
皮尔逊相关系数(Pearson correlation coefficient)
- 用于衡量两个连续变量之间的线性关系强度和方向。
- 取值范围从-1到+1,其中+1表示完全正线性相关,0表示没有线性相关,-1表示完全负线性相关。
- 适合于评估那些假设存在线性关系的数据集。如果数据中存在异常值,皮尔逊相关系数可能会受到较大影响。
斯皮尔曼相关系数(Spearman’s rank correlation coefficient)
- 衡量的是两个变量之间单调关系的强度和方向,不要求变量间的具体数值关系为线性。
- 它通过首先将原始数据转换为秩次(即排序位置),然后计算这些秩次之间的皮尔逊相关系数来实现这一点。
- 同样取值范围从-1到+1,解释与皮尔逊相关系数相同,但它更适合非参数数据或不满足正态分布的数据,也能较好地处理包含异常值的数据集。
由于不同标签之间不存在线性关系,本文选择斯皮尔曼相关系数进行相关性计算。
本文方法
密钥距离(KD)
由上述可知,选择的标签$\hat{y}$是否正确取决于$\hat{y}$与正确标签$y^*$之间的距离,这里作者将不同候选密钥与真实密钥之间的距离称之为密钥距离(key distribution),由平方欧氏距离计算而得,公式如下:
$f$表示泄露函数,在理想状况下,假设当前$\hat{y}=y^*$,则KD=0,图3展示了不同泄露模型上计算的KD,由公式也可以推出,当使用ID泄露模型时,$KD_{ID} \gg KD_{HW}$, 由于本文中实验的数据集均服从汉明重量泄露,对此作者采用HW模型。
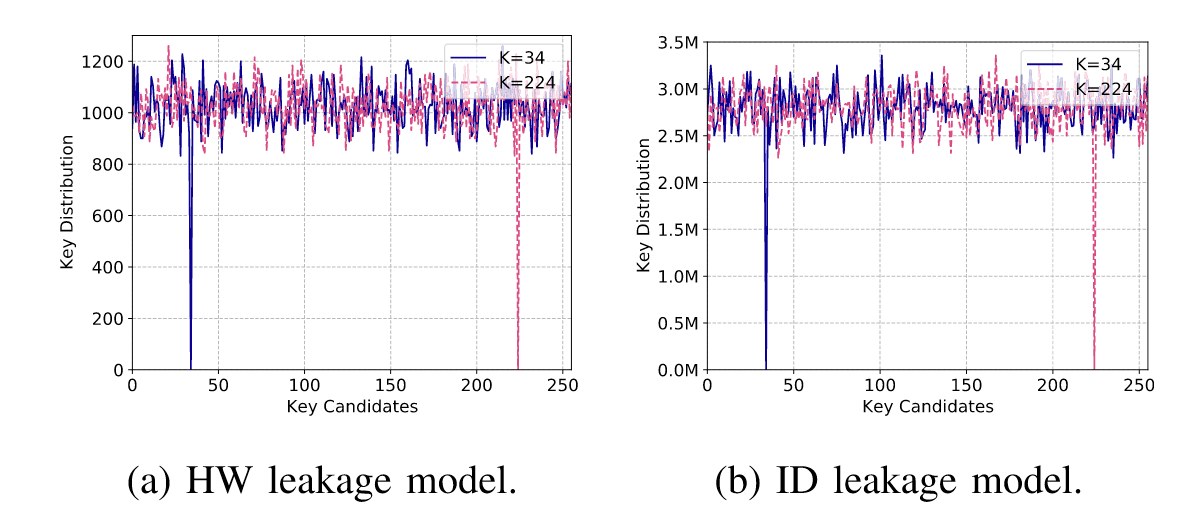
标签相关性
令猜测熵向量为$\boldsymbol{g}$,密钥距离为$KD$,标签相关性计算公式如下:
作者分别通过HW和ID两种泄露模型完成模板攻击,猜测熵以及KD对应关系如下图所示,其中蓝点为1000条训练集得到的结果,黄点为1,000,000条能量迹攻击的结果。
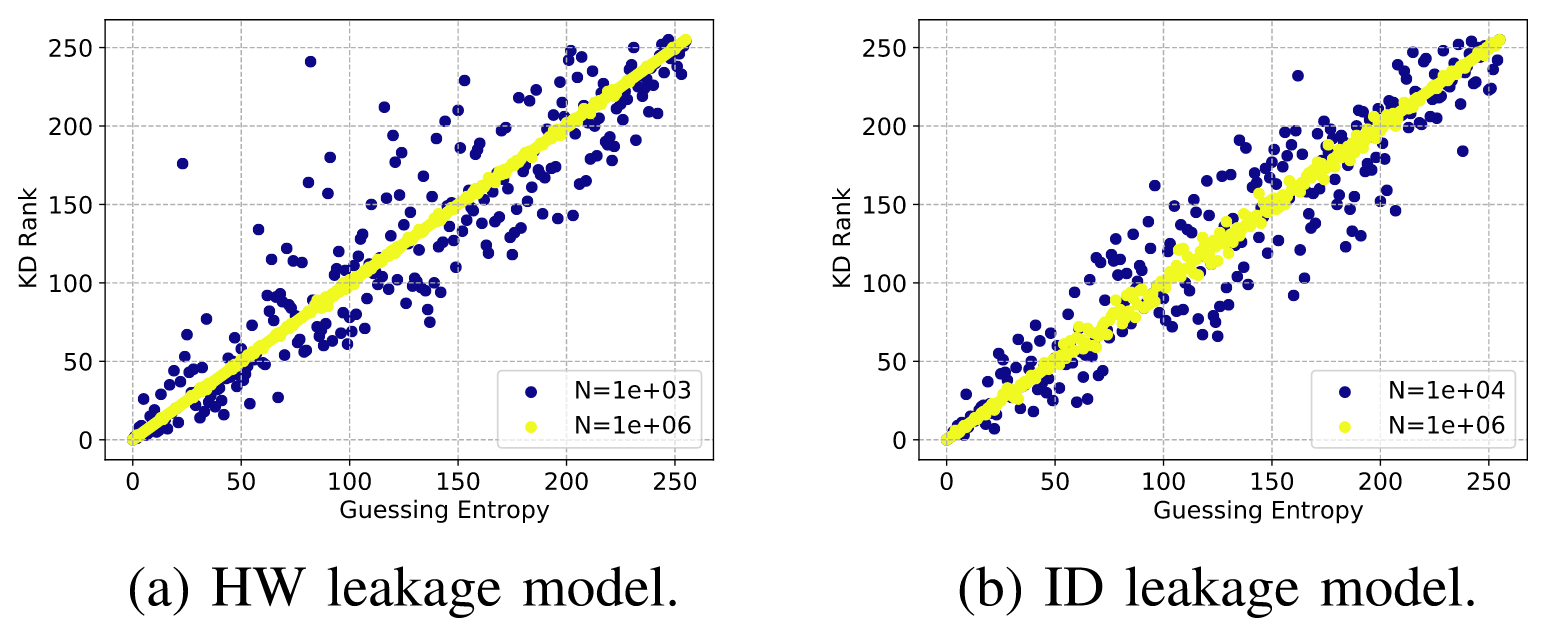
不难看出,增加训练集数量能显著增强KD与GE之间的相关性,由图3中可知正确密钥与错误密钥之间的距离并没有线性相关性,对此,作者在这里采用斯皮尔曼相关系数进行相关性计算,在HW和ID上分别达到了0.999和0.998。
实验步骤
- 选取CNN和MLP神经网络进行训练和攻击
- 搜索最佳$\sigma$的值
- 减少训练所用能量迹的数量,增加高斯噪声进行消融实验
实验结果
在图6、图7和图8中,分别展示了本文的方法在ASCAD_F、ASCAD_R和CHES_CTF数据集上的使用MLP、CNN通过汉明重量以及身份这两种泄露模型的攻击结果,当$\sigma$取0时,分布式标签表现为One-hot Encoding方法,当增大训练集时,作者采用的是Kim1等人的方法,选取的增益水平为0.25、0.5、0.75、1.0。
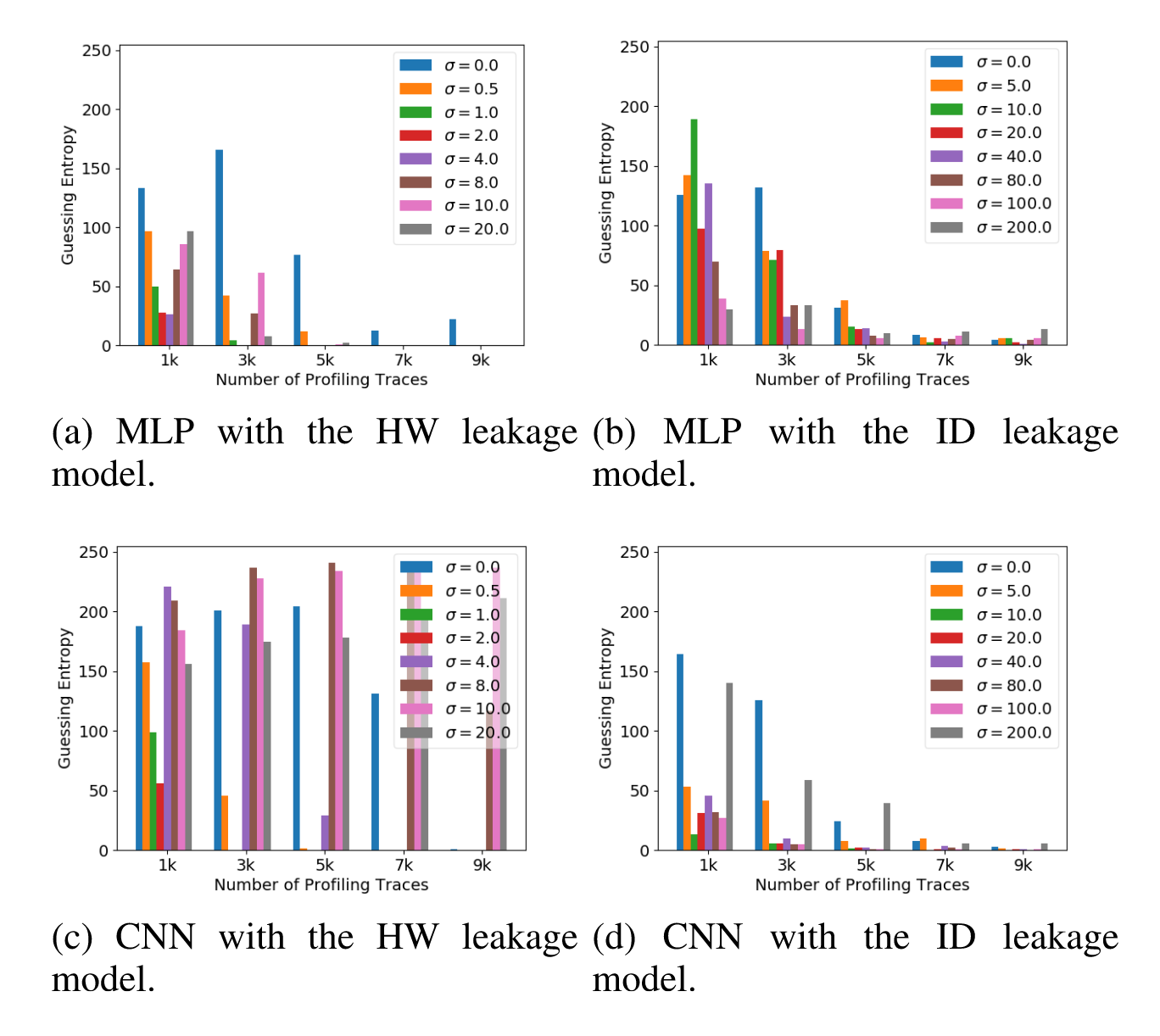
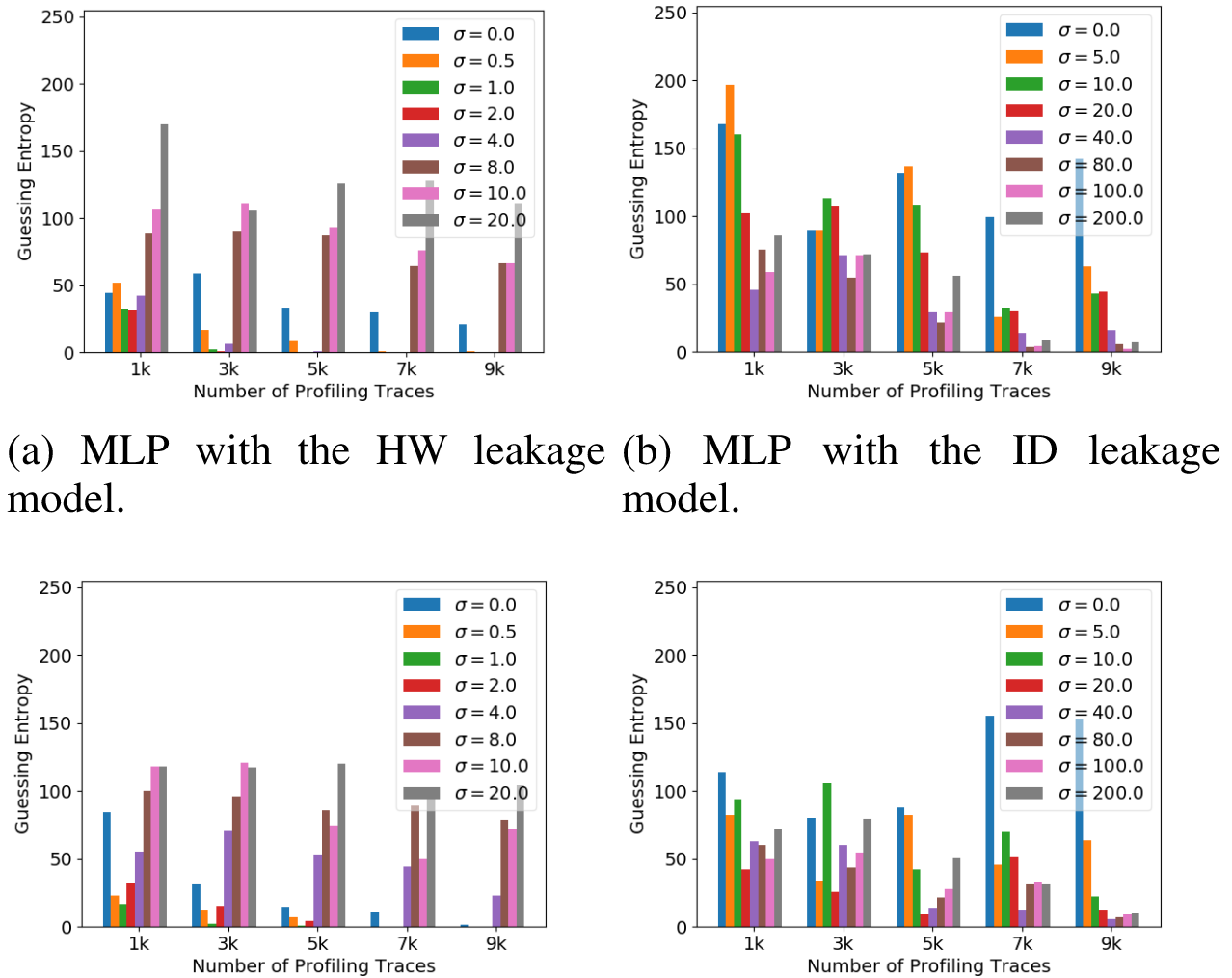
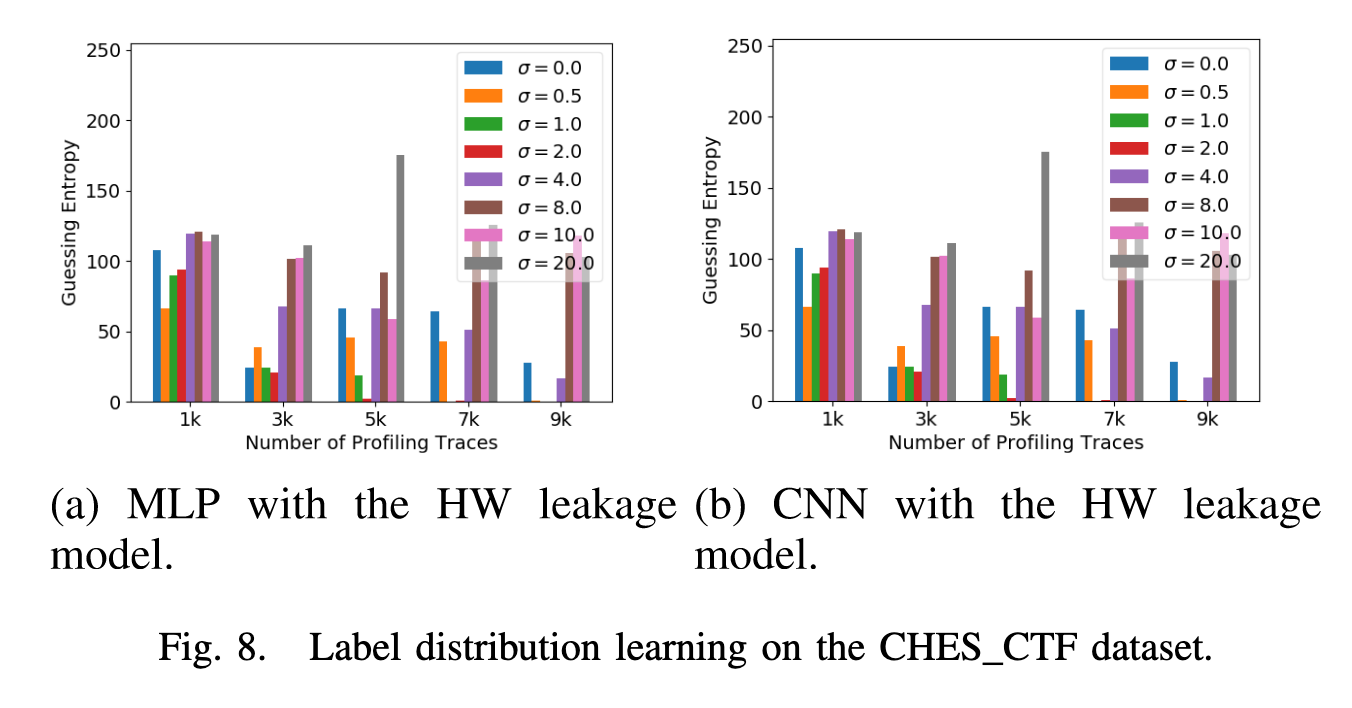
One hot Encoding结果用黑色表示,训练时作者用的损失函数是CCE,在ASCAD_F数据集上,使用本文的方法计算汉明重量泄露标签时,将猜测熵收敛到0时所需的建模能量迹可少于3000条,使用之前的独热编码则无法完成攻击。此外,实验也证明对于HW泄露模型,$\sigma$在1到2之间是最好的,对于ID则需要增加到20-80。
观察标签分布学习那一节的图可知,采用相同的$\sigma$时,ID泄露模型对应的分布范围明显很小
之后在其他数据集上同样做了相应的解释,总的结果如下表所示。
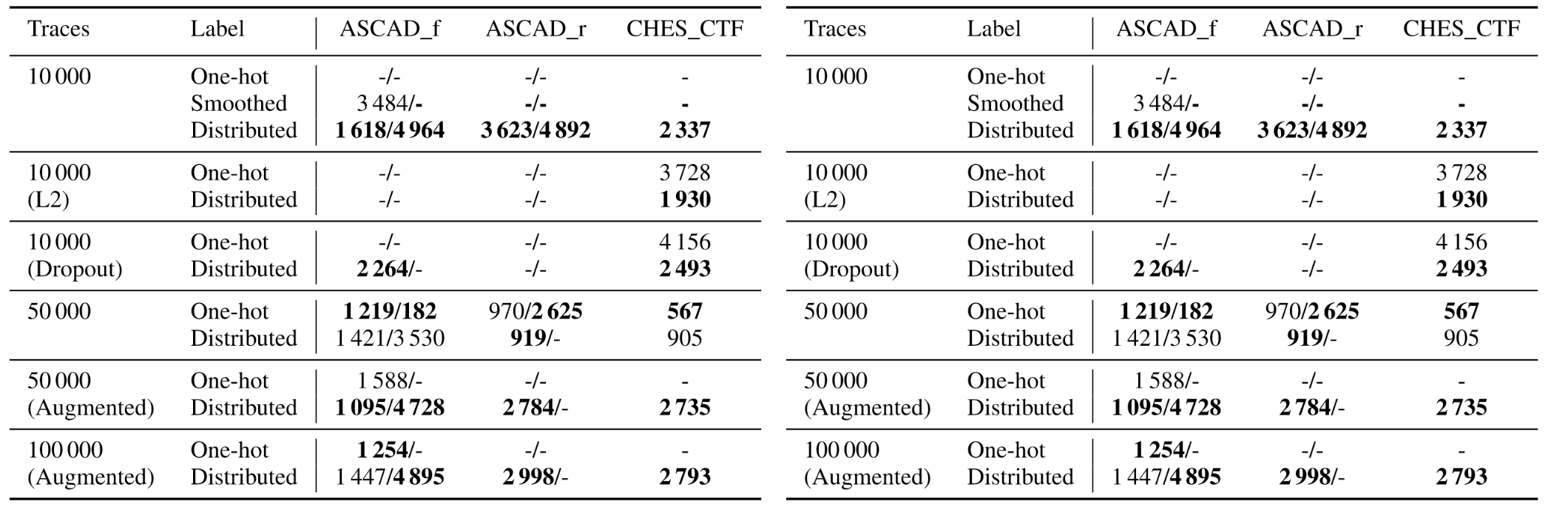
最后,作者又介绍了一种基于标签相关性的评估指标,探究了早停止、模型结构搜索对攻击结果的影响,但这里就不贴结果了,可以去看原文。
总结
这篇论文提出了一种创新的方法来提升基于深度学习的侧信道分析(SCA)效率,特别是在面对有限的侧信道泄露轨迹时。通过将传统的一热编码标签转换为分布式的标签表示,并引入键分布(KD)和标签相关性(LC)作为新的评估指标,研究展示了如何显著减少所需的配置轨迹数量同时保持或提升攻击性能。
参考文献
-
J. Kim, S. Picek, A. Heuser, S. Bhasin, and A. Hanjalic, “Make some noise. unleashing the power of convolutional neural networks for profiled side-channel analysis,” IACR Trans. Cryptograph. Hardw. Embedded Syst., vol. 2019, no. 3, pp. 148–179, 2019 ↩︎
