文献阅读笔记-Mahalanobis Distance Similarity Measure Based Distinguisher for Template Attack

M0nk3y included in 侧信道攻击

2025-03-14 About 300 words 2 minutes - views

Contents

文章信息

作者：张海龙¹，周永彬¹，冯登国²。
单位：
1. State Key Laboratory of Information Security, Institute of Information Engineering, Chinese Academy of Sciences, Beijing, China
2. Trusted Computing and Information Assurance Laboratory, Institute of Software, Chinese Academy of Sciences, Beijing, China
期刊: SECURITY AND COMMUNICATION NETWORKS

本文贡献

作者提出了一种基于马氏距离的区分器，利用该区分器来完成在不严格遵循多元高斯分布的泄露上的关键信息恢复的任务，且该方法在平均协方差上取得的表现要优于传统模板攻击。

复现地址

https://github.com/i4mhmh/easy-sca-repo/tree/main/Mahalanobis-Distance-Similarity-Measure-Based-Distinguisher-for-Template-Attack

文章内容

模板攻击

模板攻击分为两个阶段：建模、攻击。

建模阶段

随机在训练集中选择$n$条能量迹$I_1,I_2,\ldots,I_n$，对应$n$个明文$p_1,p_2,\ldots,p_n$，通过已知密钥计算中间值$v_1,v_2,\dots,v_n$,假设采用的预泄露模型为汉明重量模型，则可将能量迹分为9组$0,1,\ldots,9$。令$\boldsymbol{t}_j$表示为第$j$条能量迹$I_j$中的泄露点集合。则可构造模板$T(\boldsymbol{m}_i,\boldsymbol{C}_i)$。其中$\boldsymbol{m}_i,\boldsymbol{C}_i$计算方法如公式(1)所示。

$$ \begin{equation} \begin{aligned} \boldsymbol{m}_i &= \frac{1}{n_i} \sum_{j=1}^{n_i} \boldsymbol{t}_j, & \boldsymbol{C}_i &= \frac{1}{n_i - 1} \sum_{j=1}^{n_i} (\boldsymbol{t}_j - \boldsymbol{m}_i)^T (\boldsymbol{t}_j - \boldsymbol{m}_i) \end{aligned} \end{equation} $$

攻击阶段

同样的，随机从测试集中抽取$a$条能量迹${I_1, I_2, \ldots, I_j, \ldots, I_a}$，设候选密钥为$K_g$，计算对应的匹配概率为$P_{k_g,j} = T(\boldsymbol{m}_i,\boldsymbol{C}_i)$，具体计算步骤如公式(2)所示。

\begin{equation} P_{k_g, j}(\mathbf{t}_j; (\mathbf{m}_{k_g}, \mathbf{C}_{k_g})) = \frac{\exp \left( -\frac{1}{2} (\mathbf{t}_j - \mathbf{m}_{k_g})^T \mathbf{C}_{k_g}^{-1} (\mathbf{t}_j - \mathbf{m}_{k_g}) \right)}{\sqrt{(2\pi)^t \cdot \det(\mathbf{C}_{k_g})}} \end{equation}

最后，计算每一条测试能量迹的匹配概率$P_{k_g,1}, \ldots, P_{k_g,a}$，并通过累乘来计算最终的概率$P_{k_g}(\mathbf{t}_1,\ldots,\mathbf{t}_a;(\mathbf{m}))$，其中：

\begin{equation} P_{k_g}(\mathbf{t}_1, \ldots, \mathbf{t}_a; (\mathbf{m}_{k_g}, \mathbf{C}_{k_g})) = \prod_{j=1}^{a} P_{k_g,j}(\mathbf{t}_j; (\mathbf{m}_{k_g}, \mathbf{C}_{k_g})) \end{equation}

本文创新点

可以将公式(2)两边同时取对数，可得如下公式：

\begin{equation} \ln P_{k_g, j} = -\frac{1}{2} \left( \ln((2\pi)^t \cdot \det(\mathbf{C}_{k_g})) + (\mathbf{t}_j - \mathbf{m}_{k_g})^T \mathbf{C}_{k_g}^{-1} (\mathbf{t}_j - \mathbf{m}_{k_g}) \right) \end{equation}

这里可以将定值$-\frac{1}{2}$消去，此外，假设所有分组的协方差是相同的，则$ln((2\pi))^t \cdot \det(\mathbf{C}_{k_g})$仍然为定值，同样消去，最后得到概率计算公式（4）。

\begin{equation} \ln P_{k_g, j} = (\mathbf{t}_j - \mathbf{m}_{k_g})^T \mathbf{C}_{k_g}^{-1} (\mathbf{t}_j - \mathbf{m}_{k_g}) \end{equation}

此时马氏距离可以直接应用于公式（4）。

马氏距离（修正欧氏距离）：

$$MD(\mathbf{X}, \mathbf{Y}) = \sqrt{(\mathbf{X} - \mathbf{Y})^T \mathbf{C}^{-1} (\mathbf{X} - \mathbf{Y})}$$

马氏距离越小，向量$\mathbf{X}$和$\mathbf{Y}$相似性越高。

最后，作者将不同模板的协方差取平均来构建统一的协方差:

$C_0 = \frac{1}{n} \cdot \frac{1}{|V|}\sum^{|V|}_{i=1}n_i \cdot \mathbf{C}_i$

其中$|V|$是模板协方差个数，$n$代表能量迹数量，$n_i$代表属于某一个模板的能量迹数量

实验步骤

随机选取明文、能量迹通过预泄露模型构造模板
将所有类对应的协方差设置为$C_0 = \frac{1}{n} \cdot \frac{1}{|V|}\sum^{|V|}_{i=1}n_i \cdot \mathbf{C}_i$
随机在测试集中选择明文、能量迹i，计算其马氏距离
通过最后的计算结果，将马氏距离最小的密钥视作正确密钥

实验结果

实验环境

本文实验平台基于8位STC89C58微控制器，其时钟频率设置为22.1184MHz，用Agilent DSA90404A数字示波器进行采样，采样率设置为100ms/s。

实验内容

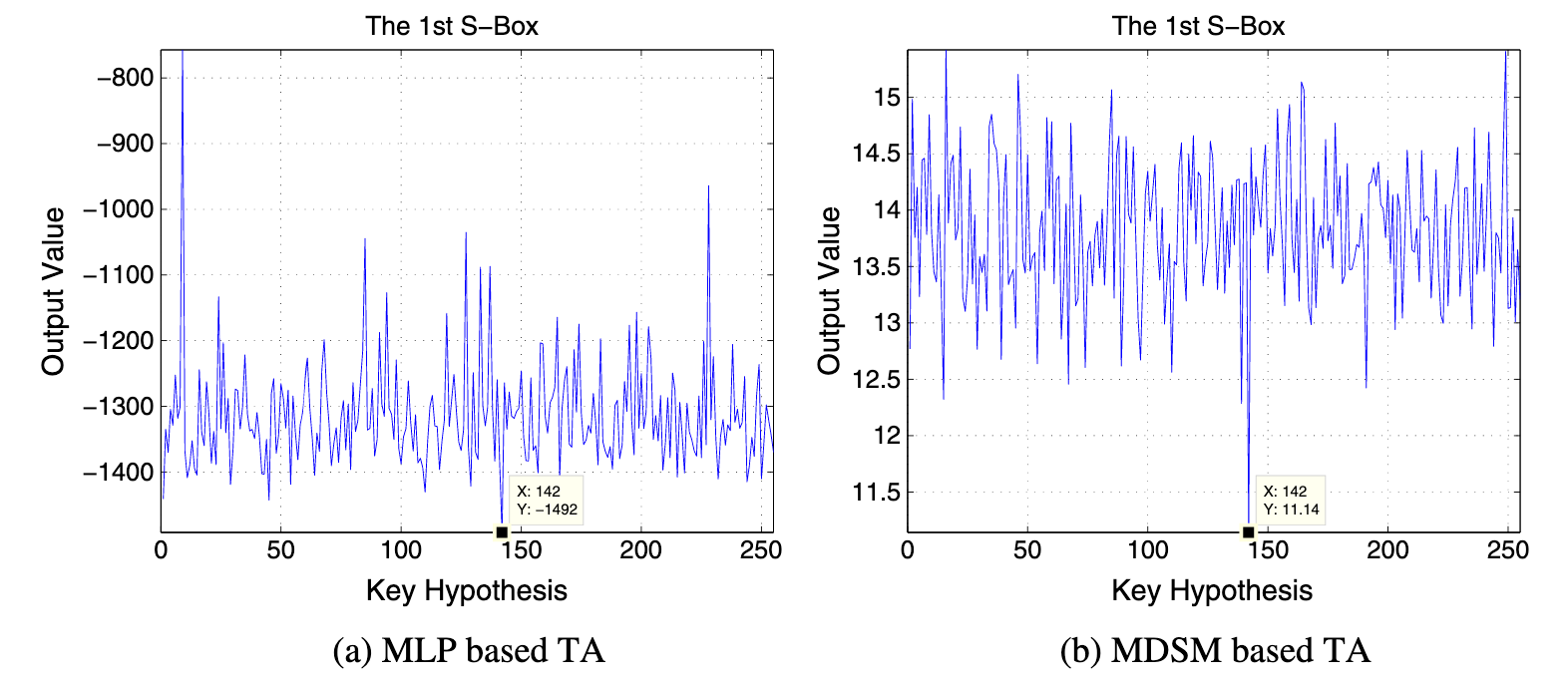
/images/image-20250316165148642.png — 图1 在8000条训练集上的攻击结果

图一展示了在8000条能量迹作为训练集的条件下，极大似然估计（MLP）以及基于马氏度量区分器的攻击结果对比，对于正确密钥，MLP的区分分数¹仅为0.6122，马氏度量区分器的区分得分为1.8983。

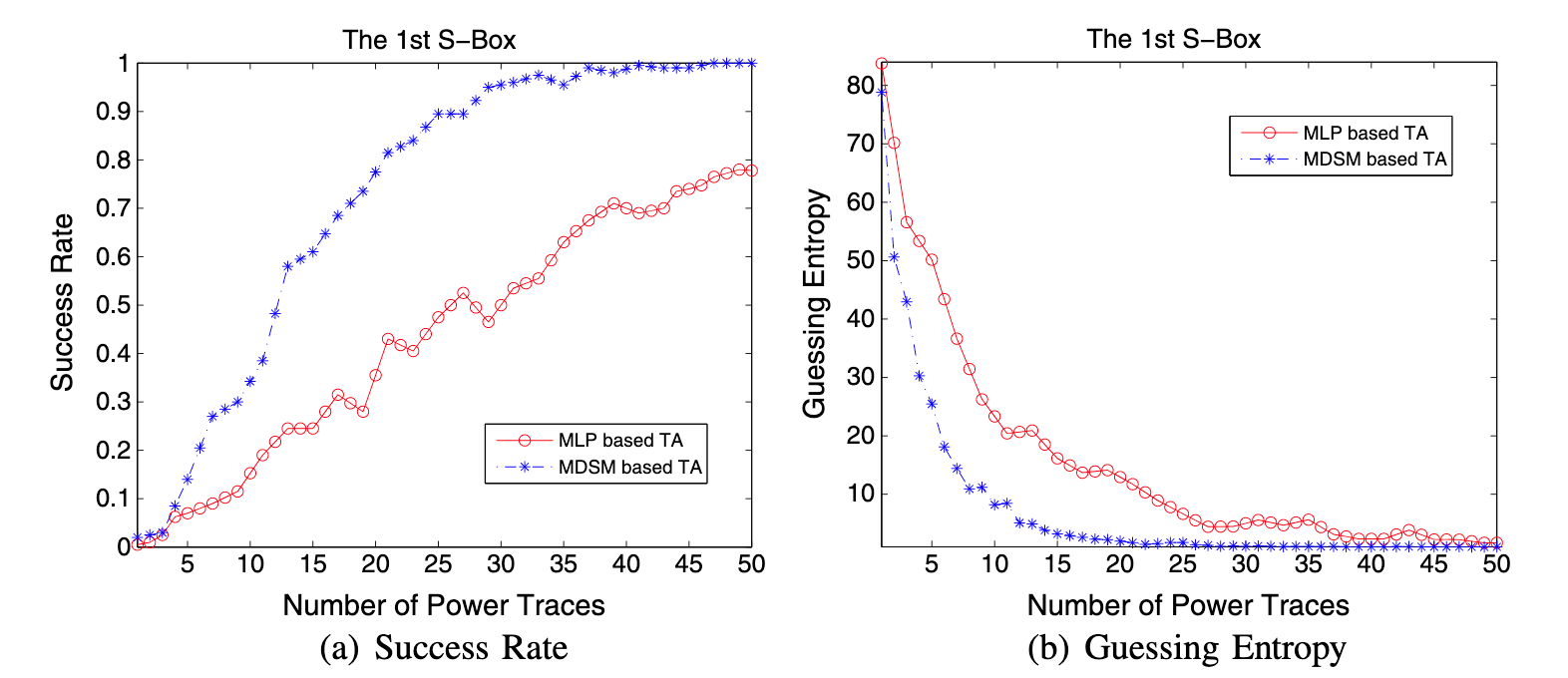
/images/image-20250316170302819.png — 图2 在8000条训练集上得到的成功率和猜测熵

在图2中，基于马氏距离的区分器（MDSM）明显优于MLP，MDSM需要20条能量迹可将猜测熵收敛到2以下，MLP则需要48条。

对比实验

作者还基于16000条能量迹上完成了模板的刻画，最后MLP需要46条将猜测熵收敛到2以下，MSDM则需要18条，其效果仍优于MLP。

后续实验

此外，作者还考虑了在严格遵循多元正态分布的能量迹上的对比实验，发现此时MLP与MDSM的效果相当，然而采用同一协方差$C_0$时，MDSM的仍然可以取得较好的攻击结果。

总结

作者提出了一种基于马氏距离度量的区分器，该区分器放宽了对能量迹泄露分布所服从的条件且更关注不同变量之间的交叉相关性，使得该方法在统一的协方差矩阵下取得更为高效的攻击结果。

Whitnall C, Oswald E. A Comprehensive Evaluation of Mutual Information Analysis Using a Fair Evaluation Framework, CRYPTO 2011, LNCS 6841. Springer: Heidelberg, 2011; 316–334. ↩︎